Background
I recently thought about the Monty Hall problem while playing the classic three shells game with my 10-year-old daughter. In case you need a refresher, the Monty Hall problem is essentially the three shells game with a twist: an object is placed beneath one of the three shells without the player seeing it, and the player chooses one of the shells where they hope the object is. After the player makes their choice, one of the shells is removed that a) wasn't the shell chosen by the player and b) also does not have the item. Then, the player is given the choice to either stick with their first choice, or change their choice to the other remaining shell.
It's an engaging thought experiment, and we had fun playing it together for a while. Fortunately, I couldn't remember if changing one's choice was the "correct" approach, or if one should stick with the initial choice. My daughter hadn't seen the game before, so we were both at least a little unbiased.
After playing for few rounds, we both decided to get "scientific" and see if we could find a way to win more often. We decided to track sticking with the initial choice (four of 10 games resulted in a win) and switching the choice (six of 10 games resulted in a win). Then, things got really interesting as we went to the computer, opened JMP, and made a simulation. My daughter knows that I work for JMP, but beyond that, she didn't really know what I do at work.
Building a model
I decided this might be a good opportunity to introduce her to using JMP to solve problems, so we built a data table together to simulate each step of the game. We started with just 10 rows, making formula columns for each of the steps. There was a bit of trial-and-error as we tested (and refined) the formulas with the cups in front of us. There were also some fun moments as I saw how quickly my daughter was learning to make formulas. She even asked me when she would get to "learn about this type of stuff in school," and when the next Take Your Child to Work day would be.
The table we came up with, pictured below and attached to this entry, is fairly simple. Each step in the process of the game is reflected in a formula column. The first columns are straightforward formulas, randomly choosing which shell the item is under and which shell the player chooses.
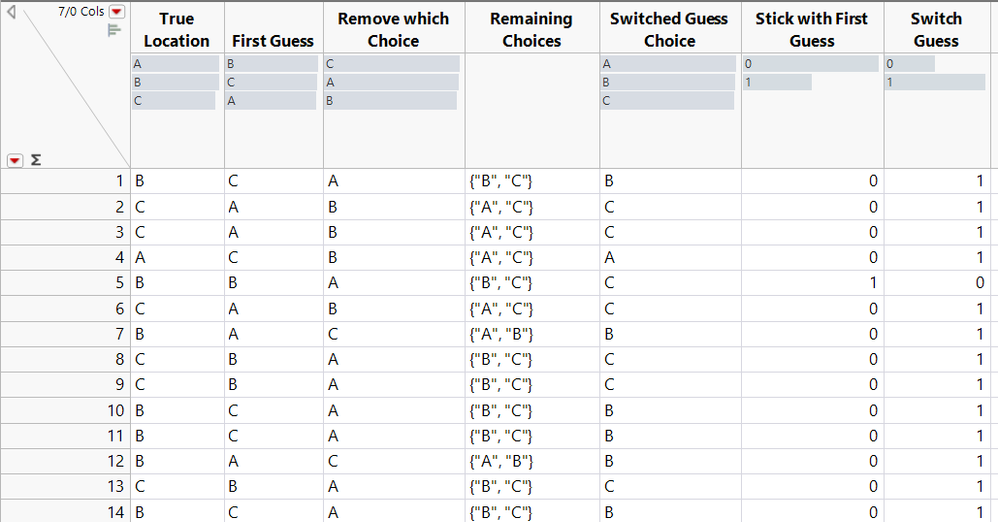
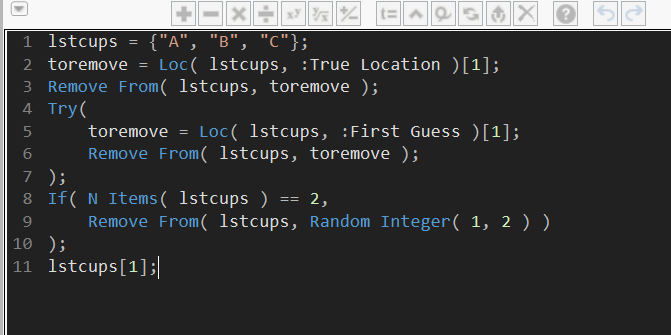
Some of the columns have more complex formulas. For example, the Remove Which Choice column formula is more like a script, including multiple steps to arrive at an output.
The last two columns reflect winning (1) or losing (0) the game based on sticking with the original guess or switching guesses.
Simulation and learning
Now that we had a model that could predict the outcome of a few experiments, we wanted to run lots of experiments to predict the general outcome. This is often called the Monte Carlo method. To simulate the outcome of many different experiments, we just needed to add many rows to our data table. Changing the table to have 10,000 rows, we quickly saw in the Header Graphs that switching is the better strategy. We confirmed this with the Distribution platform.
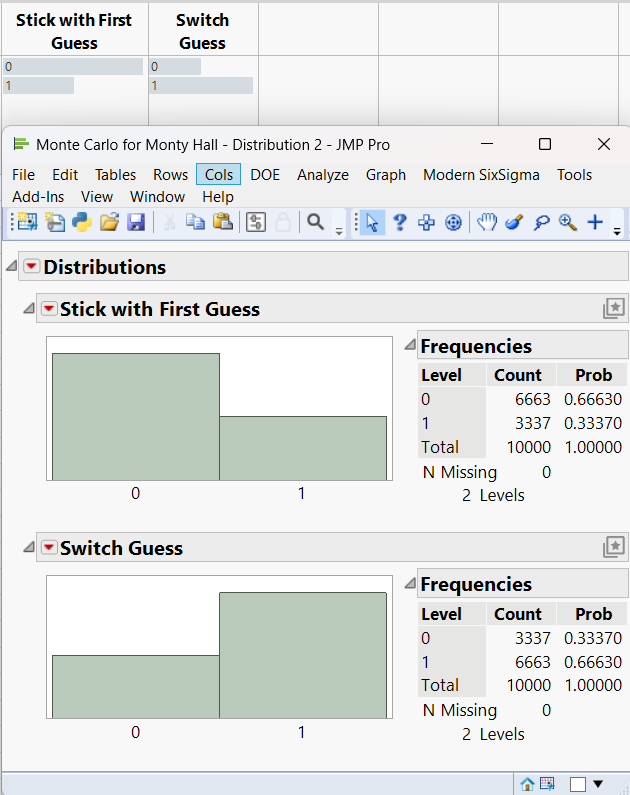
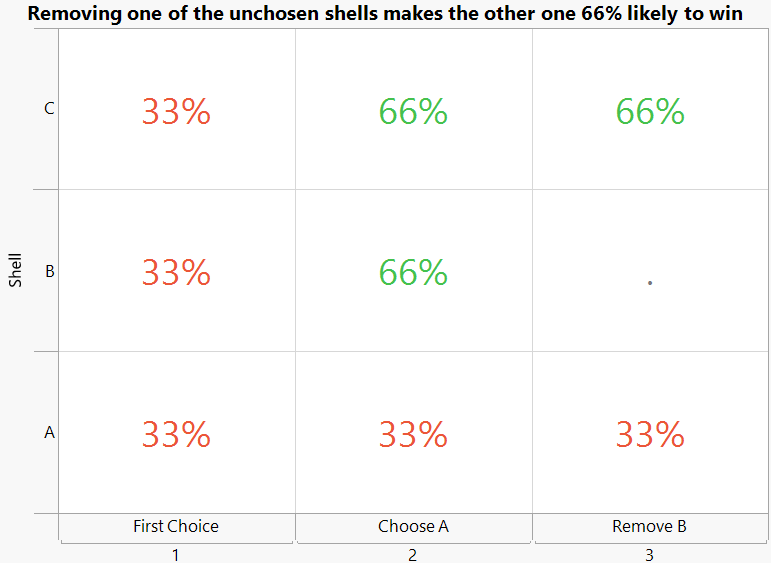
However, the 66% success rate for the switching strategy surprised me. My intuition led me to think that switching would be a 50% success rate versus 33% success rate for sticking with the first choice. As is often the case, visualizing the problem using Graph Builder helped me understand it better. The initial choice has a 33% chance of being correct, while the remaining two shells have a combined chance of 66%. Removing one of the remaining shells doesn't change that 66% chance, but it does restrict that 66% chance to just one shell.
Conclusion
Ultimately, this was an entertaining excuse to introduce my daughter to a fun topic, and a way to satisfy my curiosity at the same time. I always find it interesting how many different ways JMP can be used to investigate and solve problems. Do you have any fun experiences like this? If so, please mention them in the comments.
Monte Carlo for Monty Hall.jmp