Life Distribution – Not Just for Reliability
Created:
When it comes to distribution fitting you may feel there is a dichotomy between Distribution and Life Distribution. You may think that Life Distribution is meant strictly for reliability problems and Distribution for everything else. While Life Distribution is tailored to reliability and survival, with an emphasis on fitting cumulative distribution functions, it can also be used in situations when the available distributions in Distribution fall short. Regardless of the context in which you’re using Life Distribution, it’s helpful to know a little about the distributions it contains and how they might be applied.
Initially, Life Distribution might feel overwhelming because of the abundance of choices. Fortunately, of the 23 distributions available (plus the ability to create mixtures of distributions) there are only five fundamental distributions: Normal, Logistic, SEV (smallest extreme value), LEV (largest extreme value), and GenGamma (generalized gamma). The remaining 18 distributions can be derived from these fundamental five. First, each fundamental distribution has a logarithmic complement: Lognormal, Loglogistic, Weibull, Fréchet, and LogGenGamma, respectively. Data that fits a logarithmic complement can be transformed to its non-logrithmic predecessor by taking the (natural) log of the data values. Second, all of the logarithmic distributions, except for LogGenGamma, have three special cases to account for threshold boundaries (TH Lognormal, TH Loglogistic, TH Weibull, and TH Fréchet), zeros (ZI Lognormal, ZI Loglogistic, ZI Weibull, and ZI Fréchet), and (a single) defective subpopulation (DS Lognormal, DS Loglogistic, DS Weibull, and DS Fréchet). Mixtures can be created with any fundamental five and their log complements except GenGamma using Fit Mixture and Fit Competing Risk Mixture. Finally, the lone holdout, Exponential, is a special case of the Weibull. In this post I'll talk about the fundamental distributions and their complements, leaving special cases and mixtures for another time.
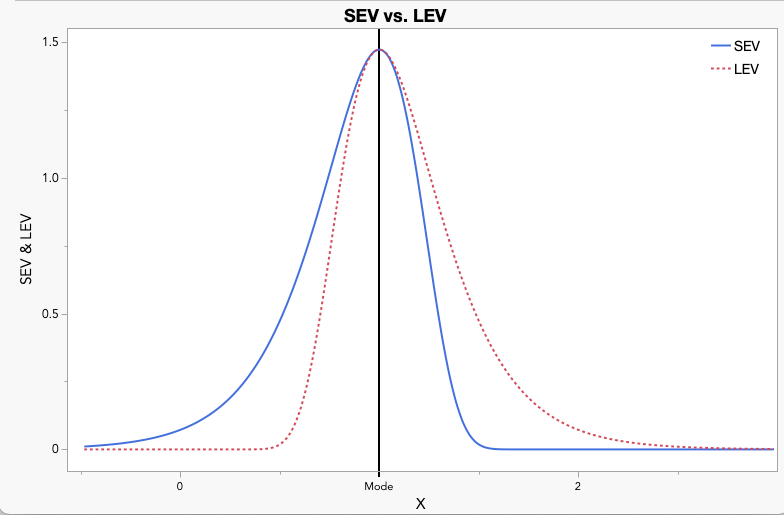
Extreme value distributions were derived in pursuit of distributions to model minimum (SEV) and maximum (LEV) values. In 1954, the National Bureau of Standards, which would later become NIST (National Institute of Standards and Technology) published an historically important document based on a series of lectures given by Emil Gumbel, Statistical Theory of Extreme Values and Some Practical Applications. It presents an early codification of extreme value theory. You can download it here. The SEV distribution is also known as the Gumbel distribution.
 |
 |
Both the SEV and LEV can be negative, depending on parameter values, making it undesirable for modeling strictly positive quantities. An interesting characteristic of the SEV is that it is left skewed, where a majority of the observations fall above the mean (i.e., the median is greater than the mean). It can be useful for modeling data with extreme left tail observations.
Example 1 – Minimum annual temperature, Austin, Texas.
Weather data, including daily temperature extremes, can be downloaded for a large number of weather stations from around the world from the National Oceanic and Atmospheric Administration (NOAA). The following data set comes from the Global Historical Climatology Network – Daily set of data and contains the minimum yearly temperature observed in Austin, Texas, from 1893 to 2022. The original data was obtained from two stations: GHCND:USC00410420 (Austin, TX US, 1893 – 1938) and GHCND:USW00013958 (Austin Camp Mabry, TX, US, 1939 – 2022).
The histogram and skewness value show the data to be left skewed.
Using Fit All Distributions shows the SEV to provide the best fit.
An assumption with any of these distributions is that the observations are independent. Using yearly data ameliorates the serial correlation that would occur with monthly extremes, as you would expect adjacent months to be more similar than months further apart. Additional factors may also come into play with this type of data making observations less independent, such as urbanization and climate change.
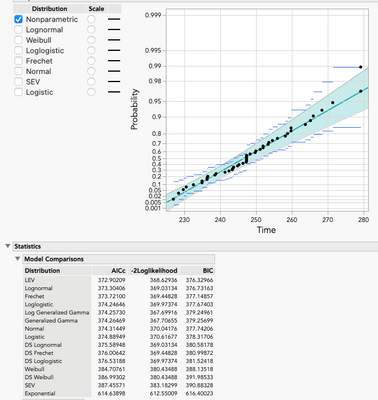
Example 2 – Progression of the fastest indoor mile run-times
The data can be found in Wikipedia (Under Men’s Indoor Pre-IAAF and Men Indoor IAAF era). The observation for Glenn Cunningham on the oversized track has been removed. Only data under the Time column was used. The results show LEV to be best with Lognormal a very close 2nd.
If the Distribution platform was used, LEV would have been missed. Notice that the AICc, BIC, and -2*LogLikelihood values match across the two platforms, making direct comparisons possible.
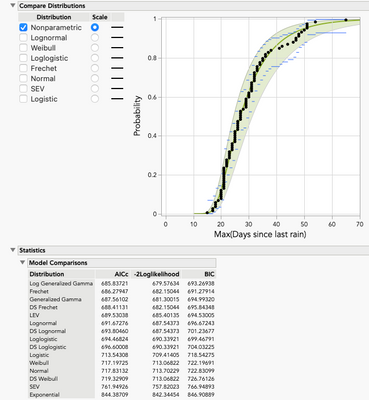
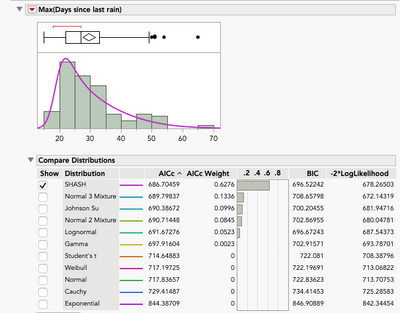
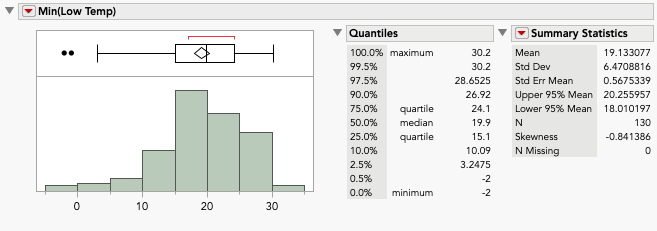
Example 3 – Maximum Consecutive Rainless Days in a Year, Austin, Texas (1927 – 2022)
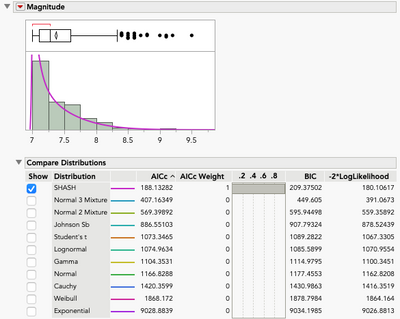
This data also comes from NOAA. The same stations and dates from Example 1 were with the data starting in 1927. Like the previous example, we will consider both the Distribution and Life Distribution platforms. Life Distribution shows Log Generalized Gamma to provide the best fit followed by the Fréchet. The SHASH (Sinh-ArcSinh) is the best fitting distribution from Distribution. Based on AICc, it would be the third best overall, albeit close to the other two in terms of fit. A general rule of thumb is that anything less than 3-5 units apart is not considered different, so we could consider any of these three distributions.
 |
 |
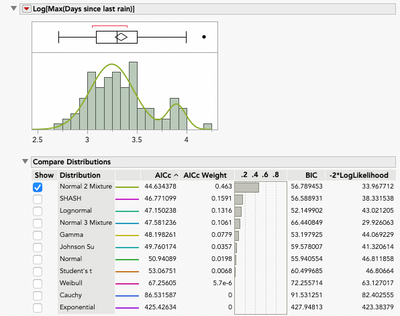
As mentioned above, the log of Fréchet distributed observations are LEV distributed. We can see this by taking the log of Max(Days since last rain) and using Life Distribution.
 |
 |
The generalized gamma (GenGamma) and log generalized gamma (LogGenGamma) contain all the fundamental distributions and their log complements except the logistic and log logistic. The exponential, Weibull, and Fréchet, and lognormal are special cases of the generalized gamma (as is the gamma, which can be found under Distribution) and the SEV, LEV, and normal are special cases of the log generalized gamma. Both generalized distributions contain a third parameter, one more than the distributions they contain. The generalized gamma and log generalized gamma reduce to their special cases when this parameter (λ) equals 1 (SEV/Weibull), 0 (normal/lognormal), or –1 (LEV/Fréchet).
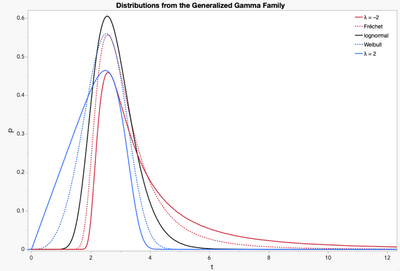
To get an idea of what flexibility the generalized distributions add, we can look at their shapes when only λ is varied. We’ll start with the generalized gamma. Setting 𝛍 = 1 and σ = 0.25, here are the Fréchet, lognormal and Weibull distributions (λ = –1, 0, 0, respectively). The probability density is on the left and cumulative distribution on the right.
 |
 |
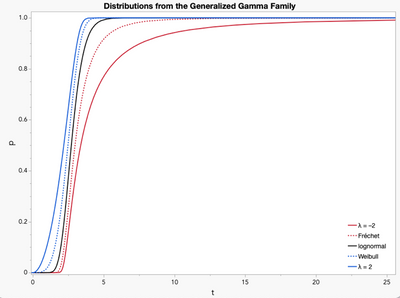The peaks (modes) are in approximately the same location. Increasing the absolute magnitude of λ spreads the distribution (i.e., it becomes less peaked, and the cumulative distribution grows more slowly). As λ gets more positive the data shifts to the right (greater probability of higher values). Decreasing λ does the opposite, concentrating more observations in the right of the distribution.
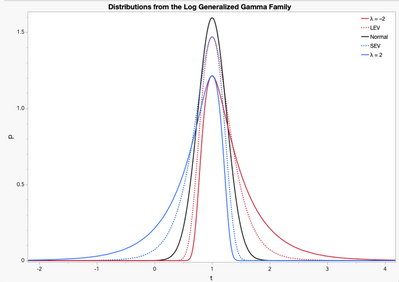
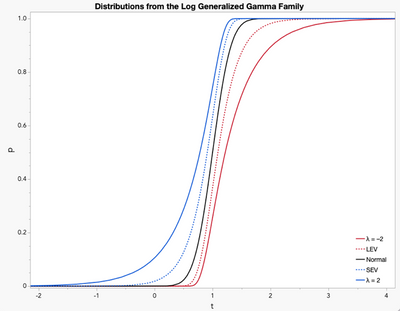
The distributions for the log generalized gamma family follow a similar pattern. The normal (λ = 0) is the most peaked (and only symmetrical member). As λ decreases from 0, the distributions become more right skewed (i.e., the concentration of observations shifts to the left with the tail to the right). The opposite is true as λ increases from 0.
 |
 |
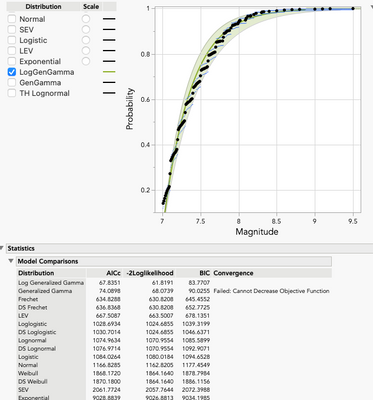
Example 4 – Distribution of Major Earthquake Magnitudes since 1800
The United States Geological Survey (USGS) makes worldwide earthquake data available for download. Since 1803, there have been 1,506 major earthquakes around the world (7.0 or above magnitude). What is the probability that the next major earthquake is 8.0 or greater?
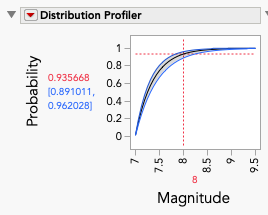
The best fit with Life Distribution is the Log Generalized Gamma. Using the Distribution Profiler, the probability of an earthquake 8.0 or greater is 0.064332 (1 – 0.935668). If we had fit the data using Distribution, our best fit would be with the SHASH, a considerable worse fit (AICc: 188.1 vs. 67.8).
 |
 |
So why bother with the special cases? A few reasons. First, people are more familiar with standard distributions like the Weibull and lognormal. Second, as lambda gets larger in magnitude, there may be instability in fitting the generalized distribution to the data. Additionally, JMP bounds λ to be between –12 and 12. For parameter values close to or at the limit, the confidence intervals can be overly wide.
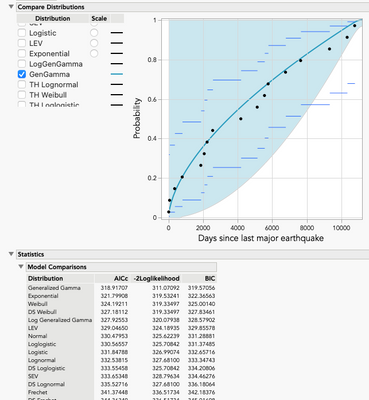
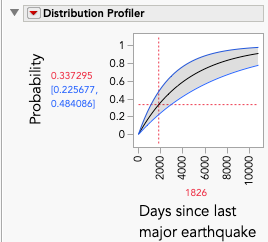
Example 4 – Predicting the next major earthquake in California
Let’s say we’re interested in predicting when the next major earthquake will occur in California. There have been 18 such events since 1803, the last one being on July 6, 2019. What is the probability of a major earthquake in the next two years? Five years?
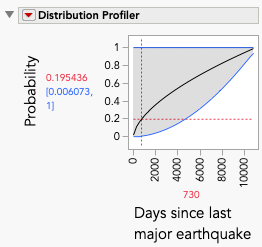
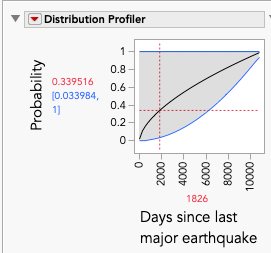
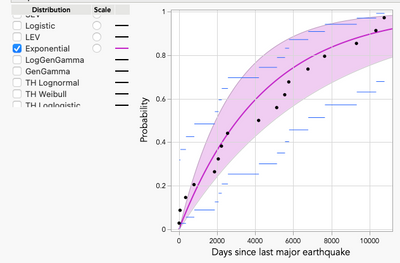
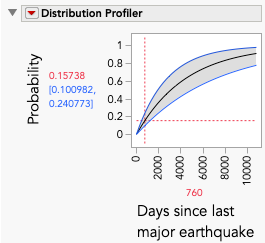
The top 2 fitting distributions using Life Distribution are the generalized gamma and the exponential. The difference between the two is about three units (AICc). We could have used Distribution and found the exponential, but it would have been more work to answer the questions. If we use the generalized gamma, we can use the Distribution Profiler to get probabilities of 0.195 and 0.339 for two and five years, respectively. Unfortunately, these are only point estimates. If we want the upper 95th percentiles confidence interval (CI) instead, we run into a bit of a problem. In both cases, the probability is 1. The wide CIs are likely due to the generalized gamma distribution having a l estimate at one of its boundaries (λ = 12). In this case, if we use the exponential distribution instead, we get a point estimate of 0.157 and an upper confidence interval of 0.24 for two years, and a point estimate of 0.337 and upper confidence interval of 0.484 for five years.
|
|
|
|
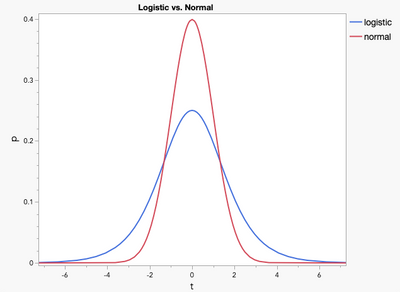
To wrap things up for this post, let’s talk about the two symmetrical distributions, the normal and logistic, and their log complements. Most of you should be familiar with the normal and lognormal, and they’re both available under Distribution. Let’s focus on the other two, the logistic and log logistic. The logistic distribution concentrates more observations in its tails than the normal. This is helpful when there are more observations in extremes than would be predicted by the normal. Below is a comparison of the normal and logistic both with 𝛍 = 0 and σ = 1.
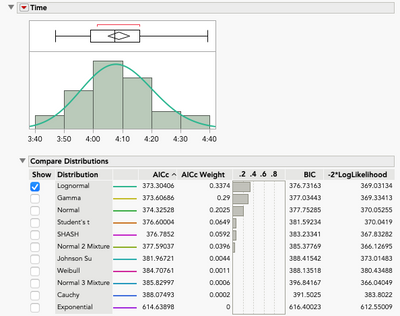
Example 5 – Monthly deviations from historical average monthly high temperatures, Austin, Texas
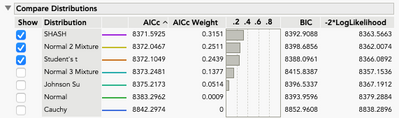
This is the same series of data as above, starting in 1893. Six months have been removed because they had fewer than half the daily observations for the month (3/1894, 6/1894, 11/1894, 9/1900, 11/1922, 8/1924). Fitting the data with Distribution shows SHASH to be the best fit, with the top four, possibly five, close enough to use interchangeably. The normal is not in this group.
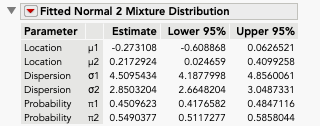
The Normal 2 Mixture fitting so well may seem to be odd at first. Looking at the parameter estimates gives insight into what’s going on. The means of the two distributions are close enough and the standard deviations different enough to suggest a unimodal distribution with heavier tails. The performance of Student’s t supports this.
Alternatively, using Life Distribution leads to Logistic having the best fit. This is appealing in that it is both unimodal and symmetric, which one might expect with deviations from a mean. While the fit is slightly inferior to Student’s t, within about 1 unit, and the SHASH, within about 2 units, it requires fewer parameters than either.
That's enough for now. In the next post I'll talk about the specialized versions of these distributions.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.