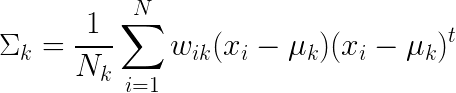JMP Blog
A blog for anyone curious about data visualization, design of experiments, statistics, predictive modeling, and more- JMP User Community
- :
- Blogs
- :
- JMP Blog
- :
- Clustering methods for unsupervised machine learning
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Report Inappropriate Content
Machine learning (ML) is a hot topic right now.
And supervised ML gets a lot of the attention. They have flashy neural networks, the Naive Bayes classifier, and lots of other sweet methods (some of which have been covered in our JMP Blog here).
But supervised ML requires labels, or truth data. We can’t ask a computer to learn what a cat is if we cannot tell it when it is correct, or incorrect. Unfortunately, labels are hard to come by in certain data sets. People have come up with ingenious ways to get labeled data cheaply, like CAPTCHAs, which ask you to click each photo that has a stop sign in it, or Google’s famous Quick Draw application; but it can be expensive to label large data sets.
Often, we don’t have labels or the truth, but we do have data. In these cases, we need to use unsupervised machine learning. Unsupervised ML is so named because we can’t tell it what is right or wrong. Just like a new babysitter who doesn’t know the rules of the house, unsupervised ML algorithms don’t have the right answers. We can’t “correct” the algorithm when it gets something wrong, because there is no clear cut right or wrong answer.
K-means
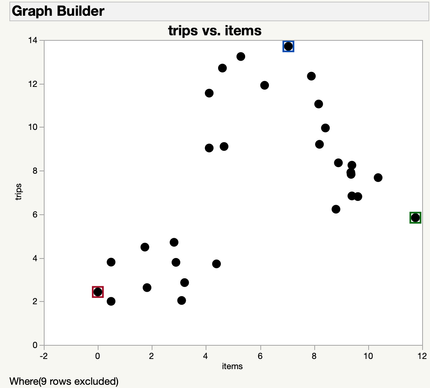
Let’s take a look at this small data set from a big department store called R.A. Fisher’s. Fisher’s is looking to implement a new three-tiered rewards program, but the staff need to know what kinds of offers to make for each of the three-tiers.
They collected pilot data about the average number of purchases and average number of items in each purchase for 30 customers. The data is graphed below.
We want to separate our customers into three groups so that we can have a tier that fits each customer. So, we decide to use k-means in order to divide the customers into three groups based on the average number of trips they make per year, and how many items they purchase on average per trip.
The first step of k-means is to pick k. We’ve chosen three. Then we pick k random points from our data. We’re going to treat these data points as the centers of our three clusters.
Then, we assign each data point to be in the cluster of the point it’s closest to. For example, this point at the top is closest to the blue point, so it will be in the blue cluster.
We assign each of our points to a cluster in this way.
Now that we have three clusters, we can re-calculate the new centers of each cluster.
And then re-assign each point to its new closest cluster.
We then repeat these steps until the cluster membership (or, the centers) do not change:
- Calculate Centers
- Reassign Points
Once this state has been reached, our model has converged, and we use these cluster memberships as our final cluster assignments.
We can now use our clusters to create our three customer tiers for Fisher’s. It looks like we have one clear group in red that has few trips, and doesn’t purchase many items. To get them in the store more often, we offer 15% off on Tuesdays.
The green group makes a moderate amount of trips, but buys a large amount of items when they do. To cater to them, our Silver tier will include coupons for 60% off one item each week to get these customers in the door more often.
And finally, our Gold tier will cater to the blue group, who come into the store regularly, but only buy a few items. This tier includes bi-annual events featuring buy one get one 50% off to try to entice these customers to buy more items.
K-means is a great way to separate your data into groups. And even though our example only had two dimensions (trips and items), k-means can work well for higher dimensional data. It’s just harder to plot the results in a blog post….
Earlier I mentioned that unsupervised learning doesn’t have any “correct” answers to compare our results with. We can’t calculate accuracy, or sensitivity. But we can calculate a measure of cohesion and separation. The most common one is a silhouette score. Silhouette scores range between -1 and 1, with higher scores being better. a(i) is the average distance between a data point, and every other data point in its cluster. This measures cohesion, how close data points in a cluster are to each other. Tightly knit clusters will have small a(i)s.
b(i) is the smallest average distance between i and each point in a different cluster. This measures separation, how separated the clusters are from each other. Clusters that are well defined will have high values for b(i) .
All together, the silhouette score for a point that is far from points other clusters, but close to points in its own cluster will have a high, positive silhouette score. Points that are closer to points in other clusters than to points in its own will have small, even negative silhouette scores.
We can get a sense for how “well” our clusters fit the data by taking an average of the silhouette scores for each data point. The silhouette score for our customer clusters (say that 10 times fast…) is 0.614, which means that our clusters are relatively cohesive and separate.
When we get high average silhouette scores, we believe that we’ve discovered some kind of latent structure in the data. If clusters are similar to themselves, and different from others, it seems like these groups are naturally occuring, not something we forced upon the data.
Expectation Maximization (with Mixtures of Gaussians)
K-means is a relatively quick-and-dirty algorithm for clustering data. It’s quick to learn, and often quick to implement. But it has two potential disadvantages: First, it assumes sphericity, meaning that the clusters are shaped like multi-dimensional spheres. In practice, this roughly means that we’re assuming that all our features have equal variance, which is often not true. Think about clustering cats based on the average number of times they meow per day, and their length in centimeters. Those two things are very unlikely to have equal variance.
The second problem is that k-means gives hard cluster assignments. Each point belongs to exactly one cluster. Sometimes, especially around the edges of our clusters, we might like to account for the fact that a point could be part of either of two clusters. Like this point here. It could be blue or green.
So when we think...or know...that our different features don’t have equal variance, or we want soft cluster assignments, we can look to a popular generalization of k-means: Expectation Maximization or EM for short.
Expectation Maximization is often implemented with mixtures of Gaussians, aka, multidimensional normal distributions. Because that’s a bit of a mouthful, we’ll refer to this technique as Normal Mixtures, because that’s what JMP calls it. We assume that all the data we observe come from k multidimensional normal distributions, and we want to figure out what those distributions are.
Just like with k-means, Normal Mixtures uses random starting points, but instead of only picking centers, it chooses a random mean and covariance for each of k distributions. At first, these might look a little wacky, but stick with us.
This is the Expectation, or E, step. Then, we calculate the probability that each point belongs to each distribution. Instead of giving each data point a hard assignment to one cluster, we say that it belongs to every cluster with certain probabilities.
Next is the M step. We recalculate the distribution parameters, just like how we calculated the new centers in k-means. Because every data point belongs to every cluster with some probability, we use every point to calculate the new distribution parameters and weight them by their respective probabilities of being in that group. A point that has only a 0.01% chance of belonging to Cluster A won’t affect the calculation of Cluster A’s mean and covariance very much. At least not compared to a point that has a 75% chance of belonging to Cluster A.
If you’re into the math, the formula for the new mean and covariance are below.
These formulas are pretty much the same as the ones we normally use to calculate means and covariance -- but with the addition of one which weighs a data point’s contribution to the calculation by how likely it is that the data point belongs to the kth distribution.
Once we have the new parameters for each of our k distributions, we perform our E step again and recalculate the probability that each point belongs to each distribution.
Then of course comes the M step, then another E step…on and on until our distributions “converge.” This either means that with each iteration of an E and M step, NOTHING changes, or at least things don’t change too much. Usually, we look at the log likelihood, and make sure it’s relatively stable.
Now we have the probability that each data point belongs to each cluster. If we need hard cluster assignments, we can just choose for each data point to belong to the cluster with the highest probability. But the nice thing about EM is that we can embrace the fuzziness of the cluster membership. We can look at a data point and consider the fact that while it most likely belongs to Cluster B, it’s also quite likely to belong to Cluster D. This also takes into account the fact that there may not be clear cut boundaries between our clusters. These groups consist of overlapping multi-dimensional distributions, so drawing clear cut lines might not always be the best solution.
Clustering in JMP
JMP has made clustering incredibly simple. All you need to do is go to the Analyze menu > Clustering. K-means and EM with Mixtures of Gaussians (called Normal Mixtures in the menu) are both offered.
Simply select either K-means or Normal Mixtures, select the columns you want to cluster on, and choose the number of clusters you’d like to find. Click Go, and you’ll have your output! If you want to save the cluster assignments, simply click the red triangle next to your cluster analysis, and choose Save Clusters!
To see a plot of your clusters, click on the red triangle and select Biplot.
If you want to try multiple k’s at a time, simply add to the Range box in the K-means or Normal Mixtures platform. Your output will now show you the information for each k! JMP will pick the best k for you Displayed under the Cluster Comparison menu.
For k-means, JMP (like SAS) uses the Cubic Cluster Criterion (that’s what CCC stands for), to select which k fits your data best. Higher CCC values are better, and indicate that your clusters fit the data well, similarly to the way silhouette scores do. JMP will pick the k that has the highest CCC value as your optimal cluster. For more on CCC, see here.
For Normal Mixtures, JMP uses the AICc (Corrected Akaike Information Criteron) and BIC (Bayesian Information Criterion) to choose the best k. Both AIC and BIC (like silhouette scores and CCC) measure how well a model (your clusters, here) fit the data. Small AIC and BIC values indicate good model fit, so JMP will chose the k that gives the lowest AIC/BIC values (note that some AICc values are missing since the data set is small).
Conclusion
Now you know how to use JMP to cluster your data using k-means and Gaussian Mixture Models (or Normal Mixtures in JMP)! So when you get a super cool data set that doesn’t have labels or truth data, you can still create some pretty cool insights using unsupervised ML.
You must be a registered user to add a comment. If you've already registered, sign in. Otherwise, register and sign in.
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us