A cringeworthy statistics statement: First in a series

[#1]

We've all heard someone say something that isn't "right." Sometimes you just let it go, either because it isn't important enough to challenge, or you don't want to cause conflict with the speaker.

This is the first of a series of statistical statements that I consider "cringeworthy." I am initially posting these statements in the Community Discussion forum to get feedback from others. Happily, several of you (shoutouts to community members @dale_lehman, @P_Bartell, @statman , @ih, @Georg, and @brady_brady) gave very thoughtful and insightful responses. Please continue the discussion! Find the second Cringeworthy Statistics discussion, which I posted today!

And read on for my take on why this first statement is cringeworthy.

Introduction

One of my "pet peeves" in the world of statistics has to do with the most basic of statements relating to a hypothesis test. Often, if a t-test (or ANOVA) ends up with a relatively high p-factor, the statistician/analyst will say, "We have p>0.05, so we can't prove the means of the two populations are different. Therefore, WE CONCLUDE THAT THE POPULATION MEANS ARE THE SAME."

The first half of that statement is correct. If p>0.05 (and we are looking for 95% confidence, and the samples come from normally distributed populations, and...), then we cannot conclude that the means of the two populations are different.

But that DOES NOT mean that the means of the two populations are THE SAME! I hear this statement all the time, even from people who should probably know better. It's just so so easy to slide right into this false conclusion. And it can be damaging, if the listener isn't familiar with statistics!

A simple example: Average height of men vs. women

As a simple example, let's say that we want to determine whether the heights of adult males is different from the heights of adult females. We have limited resources, so we can only measure the heights of three males and three females in this test. We randomly stop three males and three females on the street and measure their heights (shown below):

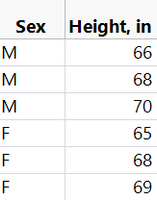
We use JMP's Fit Y by X platform to perform a t-test to compare the means of the two samples. The resulting p-value is 0.7096. Assuming we want 95% confidence in our conclusion, and since p>0.05, we conclude that we can't be 95% certain that the samples come from populations with different means. In other words, based on this sample we cannot say that men's average height is different from women's.

But this DOES NOT MEAN THAT MEN AND WOMEN HAVE THE SAME AVERAGE HEIGHT. (You can look it up... According to Medical News Today, in 2017 the average height of men was 67". And according to the Cleveland Clinic, in 2018 the average height of women was 64".)

Why did this happen? Why did the t-test not prove that men are (on average) taller than women? It is because of sampling. We can't measure all men and all women, so we chose to only sample three of each for this test. We happened to choose three men of about average height, but the three randomly chosen women happened to be a little taller than average. Combining that with the range of the measurements resulted in quite a bit of uncertainty about where the true average height of men and women might be, hence the high p-value.

Is this a "big deal?"

Yes, I believe this can indeed be a big deal! Let's take a more practical, industrial example. Let's say you have a machine that is filling vials with a powder. Your company wants to expand capacity, so you buy a second machine. You are asked to make sure that Machine B is filling to the same weight as Machine A.

You run a quick test, sampling several vials from Machine A and several from Machine B, and run a t-test. It comes back with a p-value of 0.35. Should you go to the boss and say that the machines are producing the same fill level? NO! If you do that, you risk making a mistake. If all vials coming from Machine B actually have a higher average fill weight than Machine A, then you are costing the company money by giving away "free" material. If B actually has a lower average fill weight than A, then you risk making your customers unhappy.

What can we do about it?

If you want more certainty in the averages, you would increase the sample sizes. This will also give a more accurate assessment of the comparison of men's and women's heights. But you are still faced with only being able to declare that the two populations are either proved different, or not proved different. You are not concluding that they are "the same."

You could also run an Equivalence Test (involving multiple t-tests). If interested, I would direct you here for more information. I'll leave it at that, as equivalence testing this is beyond the scope of this post.

Conclusion

So the takeaway is that while you can use a t-test (or ANOVA) to prove that something is DIFFERENT, you can't use it (by itself at least) to prove something is THE SAME. Please be careful with your terms and conclusions to avoid making mistakes in your applications!

Don't feel bad if you have made these statements in the past. In my experience, it is an extremely easy and common mistake to make. (Full disclosure: I have been guilty of making it myself!) So even though this has been said many times by many people before me, I think it bears repeating.