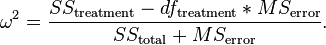Calculate Effect Sizes Add-in

[#1]

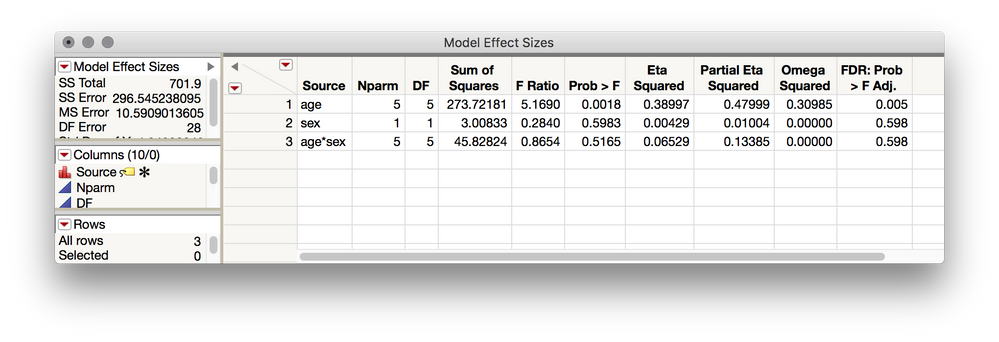
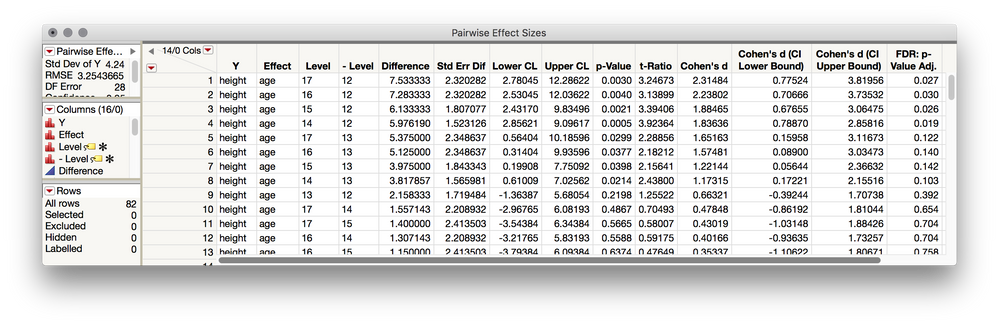
This add-in ingests estimates from an ordinary least squares report (produced by Fit Model) and saves a table of model effect estimates, F-ratios, p-values, and three measures of effect size as formula columns (Eta Squared, Partial Eta Squared, Omega Squared). If pairwise analyses are present with 'Ordered Difference' reports available, a combined data table of estimates including pairwise effect sizes (Cohen's d) will be generated, including (as of v.0.06) confidence intervals for Cohen's d. If no pairwise analyses are present this add-in will issue a prompt to add these to the selected report. As of v0.07, False Discovery Rate adjusted p-Values (Benjamini-Hochberg adjustment) are also written to the tables.

Instructions (after installing add-in):

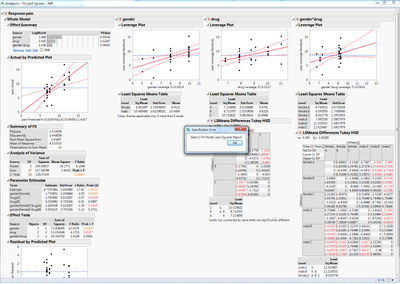
1. Fit an ordinary least squares model using Analyze > Fit Model
2. Go to Add-Ins > Calculate Effect Sizes > From Least Squares Report (Fit Model)

• If more than one Fit Model Least Squares report is open, a dialog will appear to select which analysis to use.

     For models with a categorical factor:

• If pairwise analyses (e.g. Student's t-test) and "Ordered Differences' reports are available, Cohen's d including confidence intervals for available pairwise effects will be calculated and saved to a combined data table
• If no pairwise analyses have been produced (or "Ordered Differences' reports have not been produced) a prompt will appear to add these analyses and calculate these effect sizes.Output:

• Table of model effects, effect sizes, and False Discovery Rate adjusted p-Value.

  If requested, table of pairwise effect sizes, confidence intervals, and False Discovery Rate adjusted p-Values.

  Note: Overall model statistics are saved to each table as table variables for use in formulas or additional measures of model fit you may wish to add.

Statistical Notes:

• This add-in provides estimated effect sizes, confidence intervals, and FDR adjusted p-values for ordinary least squares models (models with random effects are not supported).
• Effect Sizes Produced:

Model Effect Sizes:

Eta Squared

Partial Eta Squared

Omega Squared

• Negative values of omega squared are possible and are automatically set to 0

Pairwise Effect Size:

Cohen's d

note: In multifactor models, as well as one-factor models with more than two levels, the pooled within-cell error term of the model (RMSE) is used as SDpooled for calculating pairwise effect sizes. In these cases, it is typical to refer to the resulting effect sizes as Root Mean Square Standardized Effects (RMSSE). This is appropriate (and preferable) since the RMSE is the most statistically efficient (lowest variance) estimator of the population sigma in cases where the assumption of homogeneity of variance has not been violated.

Update History

• v0.03 - Added Cohen's d calculation for pairwise differences, and dialog to produce pairwise analyses if not present
• v0.04 - Added code to suppress prompt to add pairwise comparisons for models without categorical factor
• v0.05 - Fixed defect for running on Windows (Fit Least Squares reports were not detected). Added support dialog for selecting from available Least Squares reports:
• v0.06 - Added support for confidence intervals around Cohen's D
• v.0.07 - Added support for False Discovery Rate p-Values

[cparlett0]

I keep getting this error message. What should be selected? The output of the Fit Least Squares output is my active window (On a PC).

[julian]

There appears to be some differences in window naming on the windows and mac -- working on a fix for this now.

[julian]

Done! Rather than using the active window the new version searches the open windows for least squares reports. If only one is available that report will be used, otherwise a dialog will appear to select which least squares report to use.

[cparlett0]

This is Great! It's easy enough to calculate these by hand, but its even easier to have it calculated automatically! I also love that it includes Eta^2, Partial Eta^2 and Omega^2.

For those who are not familiar with these can also see how they're calculated but right clicking the column and selecting "Formula"!

[bernhard]

Thanks for this add-in, this is extremely useful. And being able to see the actual formula used is indeed a great plus.

Do you have any plans for creating a effect size add-in that also works with repeated measures or mixed models? This would be quite valuable, especially when using JMP for teaching to non-statisticians - I just discovered your repeated measures add-in, and having a way to produce effect sized more easily for repeated measures and mixed designs would be a great plus.

[julian]

I'm so glad you are finding this add-in useful!  Calculating effect sizes for mixed-models is a bit more complicated, but it's definitely something I would like to incorporate. I'll post updates here as soon as that's possible.

[bernhard]

Thanks Julian, that would be really useful! I hope JMP will incorporate and work on some of these changes themselves - overall the usability and interactivity of the interfaces is quite good, but there are a few points where it falls short (e.g., calculating effect sizes, checking for assumptions and reporting on them, mixed models (although your add-in fixes most of that issue nicely and elegantly). I'd love to use JMP for all my analyses but find myself going back to SPSS or another software for a few things, hope I won't need to any more in the near future.

[bernhard]

Hi there, 

I was wondering if there might be any updates on computing effect sizes for repeated measures or mixed models in JMP - would be super-useful! (it's a pity to have to go back to SPSS for calculating those...)

[wsmitty]

Hello,

I have used this on previous versions and just updated to 07 and now I dont get the ES calc (see pics). Also the summary data table doesnt collate either. I used the same steps as I had previously with the add-in (which I found great by the way). Yet no love on this attempt

Just wondering if there is something I am doing wrong? I have un-installed the add in and re-installed...no love.

Any help would be greatly appreciated.

CheersES OutputSummary table

[benson_munyan]

@wsmitty, @julian, I'm experiencing the same behavior. Did something break the addon or am I setting up my LSM models wrong?

[julian]

Hi @benson_munyan,

I can't replicate this issue on Windows or Mac, with either JMP 14 or JMP 13. Can you provide additional details about your setup and anything that might be unique about your data table? We'll get to the bottom of this. 

@julian

[JohanJakobsson]

Great tool. Pity random effects isn't supported. Is it possible in the future?

[julian]

It’s more complicated, but I have certainly considered adding support for models with random effects, most likely in the form of Cohen’s f^2. Is that the effect size you had in mind?

[JohanJakobsson]

Yes!

[TCM]

Julian,

Not sure why my first post didn't take...

I calculated d using the fit model route as you mentioned, vs manually from values of group means and pooled est. of standard deviation (from OneWay - comparing means of 2 groups).  The d value for the fit model was slightly lower than the manual calculation.  My original objective is to show difference between 2 group means ( I have 7 people rating a product before and after stability protocol to make sure there is no detectable difference).  Was I wrong to take the shortcut (fit model route with addin)?

[julian]

Hi @TCM ,

I think I can guess what might be happening here. Do you have more than two groups in your table, but are calculating d for the difference between just two of them? If that's the case, you were not wrong at all to go this route, and the small difference you found in the values of d you calculated is due to where the estimate for the population standard deviation is coming from. When you go the fit model route, the estimates for d are based on the pooled standard error across all groups. I have a note in the add-in description about this, but I should give it some more prominence. It says "note: In multifactor models, as well as one-factor models with more than two levels, the pooled within-cell error term of the model (RMSE) is used as SDpooled for calculating pairwise effect sizes. In these cases, it is typical to refer to the resulting effect sizes as Root Mean Square Standardized Effects (RMSSE). This is appropriate (and preferable) since the RMSE is the most statistically efficient (lowest variance) estimator of the population sigma in cases where the assumption of homogeneity of variance has not been violated."

So, if it is the case that you have multiple groups, the estimates from manually calculating d from just two of those groups, and the calculation from this add in, will differ slightly. Does this explain the difference? If not, let's dig into this and figure out what is happening.

[TCM]

Julian,

Thanks for the speedy response.  I am not a statistician (I am a data scientist, which falls under Computer Science- but people assume they are the same :)), so apologies for some knowledge gaps.

Not sure if we are using the term groups the same way.  What I have are 7 people.  These people rated a product at room temperature.  Another day, the same 7 people rated the same product but one that was subjected to accelerated aging.  The objective was to see if there were perceptible differences in product features (there are many that were rated by these people) between the room temp and aged product.  

I performed Oneway fit y by x with the feature as response and product (there are 2 levels- RT and aged).  In the fit model scheme, I did fit model with the same variables as the oneway.  I like the idea of the fit model because I don't have to manually calculate cohen's d (calculation from your "Subliminal Message" tutorial).  NB: I didn't check for normality;  I just assumed it. I figured I could since I am assuming the same in both analyses. I could send you a short dataset if it helps (only 14 rows and 1 response).

[julian]

Yes, if you can attach the data table that will help diagnose why you're getting a different estimate of d. That's a good first step.  A second consideration is whether or not this is the best way to go about analyzing these data. What you have sounds closer methodologically to a repeated measures experiment, and in that case we might want to go about analyzing these data a bit different. Seeing your data table will certainly help in assessing that.

[TCM]

Awesome! 

Sorry, I can't find the insert attachment button.  I only see insert/edit link.

[TCM]

Hi Julian,
Here it is. And I am certainly open to using the best way to detect differences between products. BTW, there are many more responses, but there is no order of importance among them that we know of.

[julian]

Hi @TCM ,

Hmm, don't see the attachment, and I think comments can't have attachments. Feel free to email me directly, Julian.Parris@jmp.com, and we can continue the conversation there, and then I'll update this thread with whatever insights we get to. 

[OliviaWen]

Hi Julian,

I followed the steps to calculate effect size in Fit Model. However, I see no output window for Model Effect Size. Any guess where I can find the window or what I might have done wrong? Thanks!

[julian]

Hi @OliviaWen, 

I'll reach out to you right now with a direct message we can figure out what is happening. 

@Julian

[Jandry]

Hi Julian,

I am having the same issue as OliviaWen with the no output of the Effect Size.

Thanks,

Jan

[OldGugga]

Julian was this issue solved? I have used the addin before but now its output is blank

Doug

[EK_HBRS]

Hi Julian - I am also running in the same issues as above - that is, it would be great if it would be possible to calculate effect sizes, and check for assumptions, while also the repeated measures or mixed models support improvements would be welcome. Currently, I need to switch to other software (JASP/Jamovi) to do that, which is a bit of a timedrain. Would be great if it could be resolved! Cheers, Ernst

[Mito]

Is there a way to get this plug in to work with a repeated measures model.  E.g., using the repeated measures add in?

[InaWanner]

Hi Julian, my data also includes repeated measurements among same rats. So as the others since 2016, I am also in need to get effect sizes (Cohen's d) for many variables. Some were measured 5 times in same rats, others only twice others only once. I can run the fit model by group and cross with time, is this taking care of the repeated measurement?

[suecharn]

Hello! I also have no output window for effect sizes. Any thoughts? @julian 

[julian]

Hi @suecharn,

Can you tell me a bit more about what kind of model you are setting up in Fit Model that is failing? At the moment, only models using the Standard Least Squares personality (and without random effects) are going to work with the Add-In. If that is the kind of model you're running, would you try running the code below to generate a simple two-way anova, and then run the Add-In to see if it still fails. That will help me track things down. 

@julian 

    //Open Data Table: Big Class.jmp
    Open( "$SAMPLE_DATA/Big Class.jmp" );


    //Report snapshot: Big Class - Fit Least Squares
    Data Table( "Big Class" ) << Fit Model(
    	Y( :weight ),
    	Effects( :age, :sex, :age * :sex ),
    	Personality( "Standard Least Squares" ),
    	Emphasis( "Minimal Report" ),
    	Run(
    		:weight << {Summary of Fit( 1 ), Analysis of Variance( 1 ),
    		Parameter Estimates( 1 ), Lack of Fit( 0 ), Scaled Estimates( 0 ),
    		Plot Actual by Predicted( 0 ), Plot Regression( 0 ),
    		Plot Residual by Predicted( 0 ), Plot Studentized Residuals( 0 ),
    		Plot Effect Leverage( 0 ), Plot Residual by Normal Quantiles( 0 ),
    		Box Cox Y Transformation( 0 )}
    	)
    );

[suecharn]

@julian, thank you for responding! Please forgive me as I am not incredibly versed in statistics so I hope I answer your question. We are running a full-factorial design (mixed model) with repeated measures via another "Repeated Measures" add-in. The model dialog does show that we have random effects, so that is most likely the issue.

Is there another way to obtain a partial eta squared value for effect size for this type of model? 

[julian]

@suecharn, Ah yes, if you're using my full factorial repeated measures add-in, that will produce a model that isn't compatible with this calculator for effect sizes.  I haven't added support for that because there is less agreement on a standard way to do this, especially given the diversity of models that are possible once you start introducing these random effects. The best I can say is to find a reference in your field for how it's done and mirror that method.

[Gayl]

I am using the add in and it is working fine for Student's t. I 

would like calculate effect sizes using ANOM? Do you have a solution?

[julian]

Hi @Gayl. There is no specific implementation for ANOM, but it's worth noting that the effect size d is a function of the observed differences between the groups relative to the variability in the original data. It's not a hypothesis test, and what hypothesis test you choose has no baring on the effect size, which means they're the same whether you end up testing the differences with a t-test, ANOM, etc.