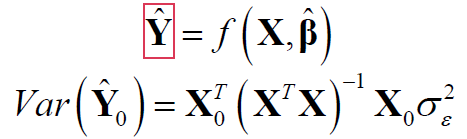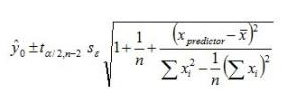- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: need error bars in arithmetic space for for a linear regression conducted in...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
need error bars in arithmetic space for for a linear regression conducted in in log space
Hi - I did a linear regression on log_turbidity (explanatory variable) vs log_ecoli (response variable) and am now trying to compute, and more importantly, understand intuitively, what my 95% confidence interval is in arithmetic space. Specifically, I need error bars in arithmetic space to go along with my back transformed predicted ecoli values, but I'm not sure how to do and interpret this step. (Note that my log-residuals are normally distributed.) Thanks in advance!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
I agree with your approach: use the transformed variables for estimating the best linear regression model, predict the mean, then back-transform the prediction to the original scale. Do the same for the confidence limits. You cannot use the JMP formula for the confidence interval, though. You need a surrogate computation.
Here is an example of what I propose:
Names Default to Here( 1 );
// example of linear regression
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
// transform varibles
dt << New Column( "Log weight", "Numeric", "Continuous", Formula( Log( :weight ) ) )
<< New Column( "Log height", "Numeric", "Continuous", Formula( Log( :height ) ) );
// fit linear regression model on transformed variables
fls = dt << Fit Model(
Y( :Log weight ),
Effects( :Log height ),
Personality( "Standard Least Squares" ),
Emphasis( "Minimal Report" ),
Run(
:Log weight << {Summary of Fit( 1 ), Analysis of Variance( 1 ),
Parameter Estimates( 1 ), Scaled Estimates( 0 ),
Plot Actual by Predicted( 0 ), Plot Residual by Predicted( 0 ),
Plot Studentized Residuals( 0 ), Plot Effect Leverage( 0 ),
Plot Residual by Normal Quantiles( 0 ), Box Cox Y Transformation( 0 )}
)
);
// save mean prediction formula
fls << Conditional Pred Formula;
// save mean confidence interval formula
mci = fls << Mean Confidence Limit Formula( .05 );
// save individual confidence interval formula
ici = fls << Indiv Confidence Limit Formula( .05 );
// proof of concept - fit polynomial function to upper mean Ci to regressor X
dt << Bivariate( Y( mci[2] ), X( :Log height ), Fit Polynomial( 2 ) );
// use back transformed value of polynomial for upper mean limit, and so on...- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
You can back-transform the values (e.g., Exp( value ) ). They will not be symmetric anymore, but they should be realistic.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
Thanks very much Mark. I have two follow up questions.
1 - Is my computed +/- error in log space the same as a percentage error in arithmetic space?
2 - Is there a way to show a 95% confidence interval in arithmetic space based on the SD of my log residuals? I'm looking for a simple equation I can use to compute the error associated with arithmetic ecoli based on my (measured) arithmetic turbidity....rather than rely on the quadratic equation used to computed the 95% CI in JMP. (I measure turbidity in real time and want to use it to estimate ecoli and upload it to a web portal in real time....my web designer doesn't do quadratic equations.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
1. I do not understand what you mean by "percentage error."
2. No. Are you considering something like a 1 or 2 SD interval? Such an interval is about the residuals, not about the predicted mean from the linear regression. the conventional intervals are not directly based on the SD of the residuals. The individual 95% confidence error bar presented with linear regression has a specific calculation and interpretation. It depends on the standard error of the predicted mean response and the associated t quantile. The standard error for a linear regression model is a quadratic form of your fitted model f and the model matrix X from the regression:
(This form is the quadratic equation you referred to.) It sounds like you won't be able to compute 95% confidence intervals as JMP does. You might be able to save the column formula for the interval in JMP and then fit a simple empirical polynomial that the web page can compute.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
Here is my JMP-produced equation for the upper 95 CI on the mean of the predicted log_ecoli:
Following up for clarity....
My upper 95% CI equation in JMP is:
1.22332500809584 + 1.09064687207089 * :log_turb + 1.97569392781527 * Sqrt(Vec Quadratic([0.0582857231016302 -0.0410476215408451, -0.0410476215408451 0.0325320549013955], [1] || :log_turb) * 0.0811942392532194)
(note the quadratic equation)
What I am trying to achieve is this: For each new measurement of turbidity, I'd like to run it through the linear regression equation (log ecoli = f(log_turbidity)) that I modeled using my training data. This will give me an estimated log_ecoli based on log_turbidity that I can back transform to get ecoli in arithmetic space. So far so good. But then I'd like to add error bars (arithmetic space) (like a 95% CI around the estimated ecoli value.....or similar approximation) to the estimated, back transformed ecoli value. If I'm understanding correctly, the error bars would have to be based on the residuals of my log-linear regression....i.e. how well the model fits the observed training data. The question I have centers around the fact that the residuals, RMSE, etc are in log space but my error bars need to be in arithmetic space. The goal is a simple approximation (or simple equation not reliant on a quadratic equation) of the expected error, in arithmetic space, plus and minus my estimated arithmetic-space ecoli.
I am told that the error in log space is the same as a percentage in arithmetic space, such that every value in arithmetic space would be in error by that same percentage. But I may not be following that correctly.
ps You mentioned fitting a polynomial function to the quadratic equation to achieve a simple equation for my web master. Can JMP do this fit and give me such an equation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
I agree with your approach: use the transformed variables for estimating the best linear regression model, predict the mean, then back-transform the prediction to the original scale. Do the same for the confidence limits. You cannot use the JMP formula for the confidence interval, though. You need a surrogate computation.
Here is an example of what I propose:
Names Default to Here( 1 );
// example of linear regression
dt = Open( "$SAMPLE_DATA/Big Class.jmp" );
// transform varibles
dt << New Column( "Log weight", "Numeric", "Continuous", Formula( Log( :weight ) ) )
<< New Column( "Log height", "Numeric", "Continuous", Formula( Log( :height ) ) );
// fit linear regression model on transformed variables
fls = dt << Fit Model(
Y( :Log weight ),
Effects( :Log height ),
Personality( "Standard Least Squares" ),
Emphasis( "Minimal Report" ),
Run(
:Log weight << {Summary of Fit( 1 ), Analysis of Variance( 1 ),
Parameter Estimates( 1 ), Scaled Estimates( 0 ),
Plot Actual by Predicted( 0 ), Plot Residual by Predicted( 0 ),
Plot Studentized Residuals( 0 ), Plot Effect Leverage( 0 ),
Plot Residual by Normal Quantiles( 0 ), Box Cox Y Transformation( 0 )}
)
);
// save mean prediction formula
fls << Conditional Pred Formula;
// save mean confidence interval formula
mci = fls << Mean Confidence Limit Formula( .05 );
// save individual confidence interval formula
ici = fls << Indiv Confidence Limit Formula( .05 );
// proof of concept - fit polynomial function to upper mean Ci to regressor X
dt << Bivariate( Y( mci[2] ), X( :Log height ), Fit Polynomial( 2 ) );
// use back transformed value of polynomial for upper mean limit, and so on...- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
Excellent - thanks so much Mark!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
WRT to your follow up question number 1: The RMSE from your log_turbidity (explanatory variable) vs log_ecoli (response variable) model is an estimate of the CV (SD/mean = coefficient of variation, sometimes called Relative Standard Deviation and often multiplied by 100 to get a %RSD) in the native scale of your response variable. So, since the +/- error in log space is a multiple of that RMSE, then it is related to % error in native (arithmetic) space.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
Thanks very much MRB3855. Please see above. You stated that " since the +/- error in log space is a multiple of that RMSE, then it is related to % error in native (arithmetic) space". Can you clarify what you mean by "since the error in log space is a multiple of that RMSE"....? I'm trying to understand this intuitively. Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: need error bars in arithmetic space for for a linear regression conducted in in log space
You'll notice the 0.0811942392532194 in your equation above. That is the RMSE^2. And, since it is multiplied within the sqrt() function, it can be factored out as RMSE. So, that complex looking equation is some number, let's call it t*C (t =1.97569392781527, the critical value from the t dist), multiplied the RMSE. Now, C, in "simple linear regression" (Y = B0 + B1*X, where Y = log_ecoli and X = log_turbidity) simplifies to something you may find manageable. C is the square root term below (the Se term is the RMSE). The denominator in the third term in the sqrt term is just the sample variance of x multiplied by n-1. The numerator of that term is the squared difference between the log_turbidity value you want to predict at and the mean of all your log_turbidity values in the data set. Then, as @Mark_Bailey indicated, just back transform the lower and upper to get back to your ecoli native scale. As he said, the resulting interval won't be symmetric (around exp(pred) ), but the percentiles carry over; i.e., the resulting Prediction Interval (PI) is a PI around the median ( exp(pred) ) in the ecoli native scale (log normal). So, you add error bars before back-transforming, not after. Note: the formula below is for a prediction interval (an interval for a single predicted value). For a confidence interval (interval for the population mean), drop the first term, the "1", from under the square root. https://stats.stackexchange.com/questions/16493/difference-between-confidence-intervals-and-predicti...
C =
You could also then get and upper "error bar" via exp(upper) - exp(pred), and a lower "error bar" via exp(pred) - exp(lower) where upper and lower are defined as in the equation above. But, they won't have the same magnitude so it isn't exp(pred) +/-error...it is exp(pred) - lower error, exp(pred) + upper error.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us