- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: how to decide the number of variables to use after principal component analy...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
how to decide the number of variables to use after principal component analysis?
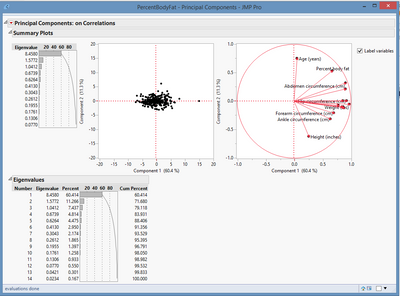
how to decide the number of variables to use after principal component analysis? I have the following result :
On basis of what parameters should I select principal components?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
I have researched some of the other articles available online regarding how to chose the components we want to retain.
Below are the suggested ways: -
1. The eigenvalue-one criterion :: In principal component analysis, one of the most commonly used criteria for solving the number-of-components problem is the eigenvalue-one criterion, also known as the Kaiser criterion (Kaiser, 1960). With this approach, you retain and interpret any component with an eigenvalue greater than 1.00
2. The scree test. With the scree test (Cattell, 1966), you plot the eigenvalues associated with each component and look for a “break” between the components with relatively large eigenvalues and those with small eigenvalues. The components that appear before the break are assumed to be meaningful and are retained for rotation; those apppearing after the break are assumed to be unimportant and are not retained.
This method was mentioned by kevin.c.anderson in the first reply to this post.
3. Proportion of variance accounted for, the criterion in solving the number of factors problem involves retaining a component if it accounts for a specified proportion (or percentage) of variance in the data set. For example, you may decide to retain any component that accounts for at least 5% or 10% of the total variance. This proportion can be calculated with a simple formula:
Proportion = Eigenvalue for the component of interest / Total eigenvalues of the correlation matrix.
What I am confused about here is that all the methods are focused around eigenvalues and not about the cumulative percentage of variance. In my current class, my professor has asked to focus on percentage. Please speak on the best way for selection of principal components.
Thank you in advance!!
P.S - the above information can be found at http://support.sas.com/publishing/pubcat/chaps/55129.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
Hi, Akshay!
Your seemingly-easy question is not so much. There are several schools of thought that yield different answers.
One school of thought says to looks at the Scree Plot.
The Scree Plot is the Eigenvalue vs. the Number of Components in the PCA. Retain the components in the portion of the steep curve, before the first point that starts the flat line trend. In these Body Fat data, this school of thought could suggest that you retain one component.
Scree Plots are often no-so-easy to interpret. One school of thought says to use your knowledge about the parameters to make a decision about the components to retain.
Another school of thought suggests "Why not retain them all?" This approach might work best a) when the number of variables is relatively small and b) when you're using the data for analytic reasons (planning action on future observations, like on control charts, etc.).
I'm sure there are even more schools of thought that might help you answer your seemingly-easy question differently.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
I agree that the seemingly-easy question is never quite so easy as one might think. Kevin points you in the right direction in terms of components. PCA reduces your large number of variables into a small number of components, looks like 1 (2 at most) is all you need.
Kevin also points out that how you proceed depends on what the end game is with the analysis.
Beyond the number of components to retain one might ask the question of how many factors do I need to build my components? This is where I utilize the ease of JMP and rerun the PCA with subsets of factors. I might look at the score plot and select one factor from each "cluster" of factors on the plot. In JMP Pro there is a "cluster variables" option that helps with understanding which variables are more like one another than others. Also, you can look at your data with different tools to best understand the relationships and importance of the variables to your end goal. This is where JMP shines, the ability to explore the data from all different angles. And besides, it is always fun to see how many JMP windows you can have open on your machine at once!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
I have researched some of the other articles available online regarding how to chose the components we want to retain.
Below are the suggested ways: -
1. The eigenvalue-one criterion :: In principal component analysis, one of the most commonly used criteria for solving the number-of-components problem is the eigenvalue-one criterion, also known as the Kaiser criterion (Kaiser, 1960). With this approach, you retain and interpret any component with an eigenvalue greater than 1.00
2. The scree test. With the scree test (Cattell, 1966), you plot the eigenvalues associated with each component and look for a “break” between the components with relatively large eigenvalues and those with small eigenvalues. The components that appear before the break are assumed to be meaningful and are retained for rotation; those apppearing after the break are assumed to be unimportant and are not retained.
This method was mentioned by kevin.c.anderson in the first reply to this post.
3. Proportion of variance accounted for, the criterion in solving the number of factors problem involves retaining a component if it accounts for a specified proportion (or percentage) of variance in the data set. For example, you may decide to retain any component that accounts for at least 5% or 10% of the total variance. This proportion can be calculated with a simple formula:
Proportion = Eigenvalue for the component of interest / Total eigenvalues of the correlation matrix.
What I am confused about here is that all the methods are focused around eigenvalues and not about the cumulative percentage of variance. In my current class, my professor has asked to focus on percentage. Please speak on the best way for selection of principal components.
Thank you in advance!!
P.S - the above information can be found at http://support.sas.com/publishing/pubcat/chaps/55129.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
There are so many ways to determine the number of factors to keep in PCA. There are even more mentioned in the JMP training course: Analyzing Multidimensional Data. Bottom line is that there is no "correct answer". It will depend on the objective of doing the analysis, what will be done with the results, the "expense" of keeping too many or too few factors. I cannot disagree with any of the suggestions already mentioned in this thread. Education of the risks, benefits, and tradeoffs is needed to make a decision that is appropriate for the given situation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
Is there a chance that the results of these three different test will be in conflict?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
Remember that PCA will always order the principal components from most variance explained to least. So, the different methods will always start "keeping" the PCs in the same order. They may disagree on where to stop.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: how to decide the number of variables to use after principal component analysis?
Akshay, in your specific case, it seems like the "best" way is the one your professor recommends!
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us