- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- deployment model
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
deployment model
Hi
to everybody.
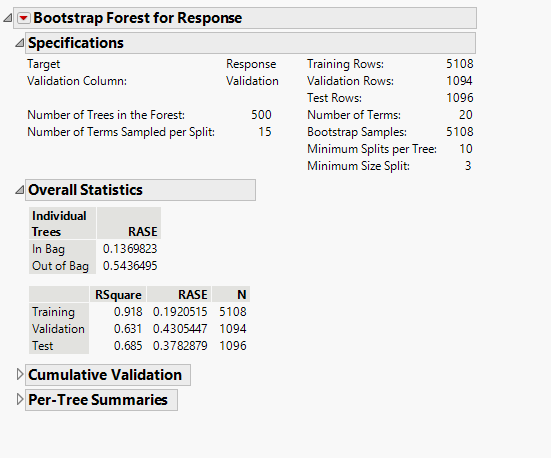
In attached 2 jmp files. The one named Training-validation-test was used to build a RF model with the following results.
The file contains one numeric response and 20 different predictors with one of them categorical, The predictors are sensors values.
As you can see the Bias is very good while the variance is slightly high (92-69=23%).
Then a new database with examples never seen by the model was used to simulate the deployment of algorithm on new data.
With high surprise the result was really poor with a R2 between the predicted and the actual response close to zero. We were not able to understand this behavior. The R2=68% for test data after all doesn't seems to be really bad. So we were expecting to obtain for sure a R2 larger than zero.
Please any help/comment is welcome.
Felice-Gian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: deployment model
Time series models are not my strength, so hopefully someone will give you a more definitive answer. I would not difference the features at first - I'd build the models and look at the residuals to see if they exhibit the same autocorrelation. If they do, then perhaps I'd try differencing some of the features.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: deployment model
Hi Dale
unfortunatly also by using the response variable difference none of the regeression models was able to return a good result.
So at this point maybe I need to assume that our X variables are not good predictors of response.
Anyway still remain the doubt if for data like ours (sensor data) we have to split the training/test by taking in account the time axis or instead we can use the random split tecnique. In the literature I found several papers where for sensor data they use the random split training/test. By if we do in the same way the results seems really good until we do the deployment of model in to production to understand that the model is completely wrong. So where is the truth?
In attached you can find a paper that apply the machine learning tecniques to a semicondcutor tool (etcher). They try to do a predictive maintenance by looking at the sensors data. So the data should be really similar to ones. If you give a look at the part hof the paper ighlighted in green looks like that they split the data taking in account the time axis and then considering the data as time series.
I hope that more people besides Dale can have their say and help us to solve this dilemma.
Are or not the data like the ours multi-time series?
It is true that the predictors X and the respone Y depend on the time. But if we want predict the Y according to the X values why the time variable should be so important? To me the Y should depend on the X variables that are set automatically by the machine during the process phase. Of course this happen in the time cronologically, but the X value depend on the recipe and machine state. So I have some difficult to accept the dependancy on the time.
Happy Easter to the whole community.
Felice
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: deployment model
I strongly suspect you need to spend more time preparing the data. To fit time series models, the observations must be equally spaced and with no duplicate time values. You have 4 sensors (?) with unevenly spaced responses. If you want to make sense of this data, I believe you need to aggregate the values so there is a single observation at each time period, and you might want to create a variable for the length of time between timed observations. I'd also suggest doing a separate analysis for each type of sensor rather than using sensor as one of your features, as the behavior of each appears to be different.
I wouldn't be prepared to conclude that your features are not predictive - I think too much noise is introduced by mixing the sensor types as well as having nonstandard time intervals. If you address these issues, there may be a good predictive model yet. The modeling part is not the problem - the data preparation is (as is often the case). At least that is what I think.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: deployment model
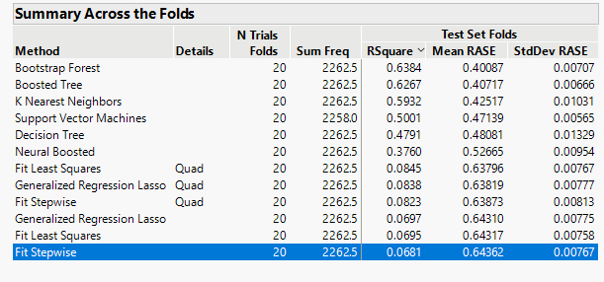
Mybe this can help in the discussion. I used the excellent model screening option in jmp pro by using the nested option to tune hyperparameters combined with the k-fold cross validation. Here the results obtained after some hour.of jmp work
What was surprising me is the large difference among the models in terms of performances. The tree models and KNN showed a R2 above 50% while all the fit models showed values well below the 50% (close to zero) even though the lasso and ridge regularization usage. Mybe is this difference that explain the bad performance of RF/Boosted models once deployed in production?
What do you think? Any comment/suggestion/help?
Felice.
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us