- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Why there is a constant component in the PCA formula
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Why there is a constant component in the PCA formula
I have been surprised to see a constant component in the saved formula when performing PCA analysis. For example, saving the 1st 2 Principal Components on the following standardized data set (centered and scaled data),
| Standardized (Centered + Scaled) Data | |||
| SLength | SWidth | PLength | PWidth |
| 0.27 | 0.19 | -0.36 | -0.44 |
| -0.30 | -1.14 | -0.36 | -0.44 |
| -0.88 | -0.61 | -0.94 | -0.44 |
| -1.16 | -0.87 | 0.22 | -0.44 |
| -0.02 | 0.46 | -0.36 | -0.44 |
| 1.13 | 1.26 | 1.38 | 1.48 |
| -1.16 | -0.07 | -0.36 | 0.52 |
| -0.02 | -0.07 | 0.22 | -0.44 |
| -1.74 | -1.41 | -0.36 | -0.44 |
| -0.30 | -0.87 | 0.22 | -1.40 |
| 1.13 | 0.72 | 0.22 | -0.44 |
| -0.59 | -0.07 | 0.80 | -0.44 |
| -0.59 | -1.14 | -0.36 | -1.40 |
| -2.02 | -1.14 | -2.11 | -1.40 |
| 2.28 | 1.52 | -1.52 | -0.44 |
| 1.99 | 2.59 | 0.22 | 1.48 |
| 1.13 | 1.26 | -0.94 | 1.48 |
| 0.27 | 0.19 | -0.36 | 0.52 |
| 1.99 | 0.99 | 1.38 | 0.52 |
| 0.27 | 0.99 | 0.22 | 0.52 |
| 1.13 | -0.07 | 1.38 | -0.44 |
| 0.27 | 0.72 | 0.22 | 1.48 |
| -1.16 | 0.46 | -2.69 | -0.44 |
| 0.27 | -0.34 | 1.38 | 2.43 |
| -0.59 | -0.07 | 2.55 | -0.44 |
| -0.02 | -1.14 | 0.80 | -0.44 |
| -0.02 | -0.07 | 0.80 | 1.48 |
| 0.56 | 0.19 | 0.22 | -0.44 |
| 0.56 | -0.07 | -0.36 | -0.44 |
| -0.88 | -0.61 | 0.80 | -0.44 |
| -0.59 | -0.87 | 0.80 | -0.44 |
| 1.13 | -0.07 | 0.22 | 1.48 |
| 0.56 | 1.79 | 0.22 | -1.40 |
| 1.42 | 2.06 | -0.36 | -0.44 |
| -0.30 | -0.87 | 0.22 | -0.44 |
| -0.02 | -0.61 | -1.52 | -0.44 |
| 1.42 | 0.19 | -0.94 | -0.44 |
| -0.30 | 0.46 | -0.36 | -1.40 |
| -1.74 | -1.14 | -0.94 | -0.44 |
| 0.27 | -0.07 | 0.22 | -0.44 |
| -0.02 | 0.19 | -0.94 | 0.52 |
| -1.45 | -3.01 | -0.94 | 0.52 |
| -1.74 | -0.61 | -0.94 | -0.44 |
| -0.02 | 0.19 | 0.80 | 3.39 |
| 0.27 | 0.99 | 2.55 | 1.48 |
| -0.59 | -1.14 | -0.36 | 0.52 |
| 0.27 | 0.99 | 0.80 | -0.44 |
| -1.16 | -0.61 | -0.36 | -0.44 |
| 0.84 | 0.72 | 0.22 | -0.44 |
| -0.02 | -0.34 | -0.36 | -0.44 |
The formulas are as follows:
Prin1: 0.59834170442161 * :SLength + 0.569834108206745 * :SWidth + 0.371661472844918 *
:PLength + 0.39892861952586 * :PWidth + 2.15154543958667e-16
Prin2: -0.331623960696996 * :SLength + -0.436415344018397 * :SWidth + 0.620670317712319
* :PLength + 0.54252700661609 * :PWidth + (-1.4778627619204e-16)
Even though the two constant components are almost close to 0 (BTW, I saw constant >> 0 in some other cases), I just don't understand why they would be part of the formula in the 1st place since Prin1 and Prin2 should be just the product between 1st and 2nd eigenvectors and the data.
In matlab, the detailed calculations will be as follows:
[U S V] = svd (cov(X));
Z2 = X * U(:,1:2) ;
Prin1 = Z2(:,1);
Prin2 = Z2(:,2);
Look forward to your explanation and thanks much in advance!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why there is a constant component in the PCA formula
The data that you provided does not have means of 0 and standard deviations of 1. Like the constant in the PC, they are close, but they are not exactly 0 and 1. That alone can give you the constant term in the PCs.
Even if the means and standard deviations were exactly 1, you may possibly get a constant term that is VERY close to 0 due to round off error and the estimation process that is being used. Regardless of your input data, JMP will be scaling your variables unless you tell it not to do so.
If you absolutely do not want the constant term, go to the red popup menu and choose to form the PCs "On Unscaled" variables. This is typically not recommended, but this will give you PCs with no constant term.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why there is a constant component in the PCA formula
As indicated, the data was standardized (centered and scaled), thus, it does have mean of 0 and std dev of 1. I did try out the "unscaled" option and indeed the constant term disappeared.
However, I still can't wrap my mind around it given that the principal components are derived from the product of eigenvectors and the data. Many thanks for the reply though.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why there is a constant component in the PCA formula
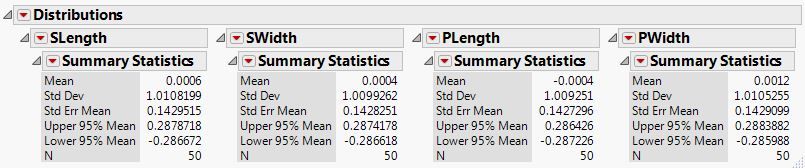
Using the data you provided, I used Distributions to look at it and got these results:
That is enough of a difference to give round-off error. Again, even if the standard deviation is exactly 1, you will likely get a constant term that is very close to zero. The scaling is what prevents everything from just being a product of the eigenvectors and the data. You are not just using the data, you are using scaled data (every time JMP will do the scaling because, as your data shows, you don't always know the standard deviation = 1). Estimation can be a messy game sometimes.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us