Why does the interaction between a squared term and a main effect always correlate with the main effect?

[#1]

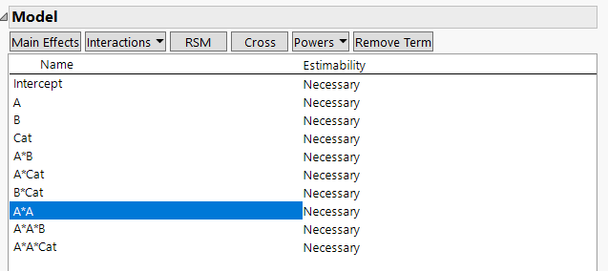
I am setting up a custom experimental design with three factors, two continuous and one categorical. I want to look at main effects, one way interactions and a squared term for one of the continuous factors, this is all fairly straightforward. What I also want to look at is the interaction between the main terms and the squared term. To me this means how the level of a given factor affects the form of the curvature described by the squared term.

For the following factors I therefore have the subsequent dialogue in the custom design view.

A: Continuous

B: Continuous

Cat: Categorical, 2 level

However, when I construct the design, no matter how many runs I decide on the correlation map shows very high (~0.8) correlations between:

B and A*A*B

Cat and A*A*Cat

Can anyone help me out as to why this is, whether it's an issue and if there is a workaround. My initial thought is that as A*A will always have a positive sign the sign of A*A*B will always have the same sign as B (and equivalently for A*A*Cat and Cat). 

Many thanks,

Dave

[#2]

Hi @david_gillespie ,

  I believe the high correlation is because there's already the other term in there for the interaction term. For example, the color map is showing that B with A*A*B has high correlation and this is because B is in that mixture term: A*A*B. B will always correlate with B, hence the diagonal is 1 in the color map. This is the same for A with A*A*Cat, A always correlates with A, so you have high correlations with those.

  There is no way to get around this because terms always correlate with themselves. Are you sure those mixture terms are real and need to be included?

Hope this helps,

DS

[#3]

Hi DS,

Thanks for the response. This is what I was getting at in my original post regarding the sign of the A*A portion of the interaction term, because although B is contained within A*B, B does not correlate with A*B. Is it that, for example, B*A does not always correlate with B because the sign of A determines the sign of the interaction term?

For simplicity, consider the following example.

Term	A =1, B = 1	A = 1, B = -1	A = -1, B = 1	A = -1, B = -1
A	1	1	-1	-1
B	1	-1	1	-1
A*B	1	-1	-1	1
A*A	1	1	1	1
A*A*B	1	-1	1	-1

Hence there is no combination of A and B where the sign of A*A*B does not equal the sign of B. Whereas for A = -1, B=1 or A = -1, B= -1 the sign of A*B does not equal the sign of B.

Whether the terms are real is obviously not certain, however it seems reasonable to me that the level of one variable (B) might affect the form of the effect described by the quadratic term of another (A*A). In this instance I know that A*A and B are both significant from previous experiments. Or is this phenomenon contained within another part of the model?

Thanks,

Dave

[#4]

Note that the parameterization of the linear predictor by JMP is not low = -1 and high = +1. See this section of JMP Help for details. The difference in the parameterization is important if you calculate the correlation between two columns in the model matrix.

I set up the factors and model to match your requirement. I used the Default = 16 number of runs. Here is the design:

 Assuming that the real effect modeled by each term is twice as large as the standard deviation of the response, I get this power analysis:

So while the correlation is high for some parameters, they are still estimable if large enough. The correlation will, of course, inflate the variance of the estimates, as shown in the estimation efficiency:

Do you expect large effects, compared to the SD?

[#5]

Hi @david_gillespie ,

  It sounds like you might be getting confused with how JMP performs it's coding/parameterization behind the scenes as @Mark_Bailey points out, or what the coefficients/signs for the factors A and B are. The coding -1/1 is the low/high coding in JMP and not the coefficients for the factors. That would only be determined after performing the DOE and then running the Fit Model on the results. The response is what tells you HOW A and B might interact or self-interact, and it gives you the sign of the coefficients for the terms that you propose in the model. If a term you propose is not relevant, it will have a large p-value, and the standard error on the estimate (for the coefficient of the term) will be larger in magnitude that the magnitude of the term itself. For example, if you get an estimate for the A*A*B term that is -2.2 and the standard error is 5 (5 > |-2.2|), then you know that term doesn't have any significant influence on the response and you can remove it from the model.

  In your example above, it appears as if you KNOW the sign of the coefficient of each term. The resulting sign of any of those combinations that you propose is entirely dependent on how many negatives and positives you are multiplying together, so no surprise there. No phenomenon to try and describe.

  If you have reason to believe that B truly affects the self interaction term A*A, then B and A are not truly independent variables. If B affects A*A, it must also affect A to some degree. If not, how could B affect A*A?

  If you have two truly independent factors, like temperature (A) and time (B), then there will be no correlation between them. However, there might be some other term, like energy (C) a covariate, which is some combination of A and B, such as A*B or A+B. In that case, C would always be correlated with both A and B. So, in this case, the main terms A and B are uncorrelated, and the mixed term C would be correlated with A and B. So those mixture terms: C*A (e.g., A*B*A) or C*B (e.g., A*B*B) would always have some correlation in it.

Hope this helps,

DS

[#6]

Hmmm, not so sure about your conclusions "If you have reason to believe that B truly affects the self interaction term A*A, then B and A are not truly independent variables. If B affects A*A, it must also affect A to some degree. If not, how could B affect A*A?".  Perhaps I am misinterpreting your comments...

The question is does the quadratic effect of A vary or depend on the variable B?  Can the curve be different with different levels of B?  This is the definition of an interaction.  A and B can be completely independent, but there can still be this interaction effect.

Multicollinearity can be assessed turning on the VIF common in your parameter estimates table and of course by doing scatter plots in the multivariate methods>multivariate platform.

[#7]

I agree with @statman in that the factors / variables are independent. That is to say, you are not constrained to changing one factor based on the level of the other factor. On the other hand, the effects of these factors / variables are not independent or additive. The interaction means that the effect of one of the factors depends on the level of the other factor.

Just trying to keep the ideas and terminology clear for everyone.

[#8]

I fully agree, there is no constraint on changing one factor versus another, but both A and B are continuous factors and if B interacts with the self-interaction term of A*A, then it must interact with the self term A.

As with my previous example., if you take A = Temp and B = Time, then there is no constraint (in principle) that limits one setting for any other possible setting of the other. If you find that your outcome depends on A*A, meaning Temp*Temp, AND you find that there is a meaningful term (A*A)*B, this would mean your outcome depends on (Temp*Temp)*Time. If Time somehow interacts with the self-interaction of Temp*Temp, it must also interact somehow with Temp on it's own. In this example, you can't physically have Time interact with (Temp*Temp) without also somehow interacting with Temp alone. It wouldn't make sense for Time to interact with the response's curvature with Temp without also interacting with the response's slope with Temp.

[#9]

Sorry, I may be confused by your statements...what is a " self-interaction term"?  If it is A*A, that is the quadratic effect of A or the non-linear effect of A. Perhaps this should not be discussed in the open forum, but I have to disagree with you.  Just because the quadratic effect of a variable (say A^2) depends on the level of another factor (say B), does NOT imply (nor require) there must be an interaction of the linear effects (A and B: A*B).  Think of the quadratic effect as departure from linear.  If the departure is greater at one level of B than it is at another level of B, that is the interaction (A^2*B).  The slopes could be negligible.  Of course, in general we follow the principle of hierarchy, and there may be first order and second order linear that seem likely should a non-linear or or other higher order effect be significant....I'll leave it at that.

But I digress..apologies the the OP.

[#10]

Firstly, thank you to everybody for their helpful, this has turned into quite the debate!, I shall try to reply to all of the various points that you have raised.

In response to your statement on the power analysis @Mark_Bailey, does that therefore mean that provided that the correlation between different estimates is not 1 then the parameters can be estimated provided that the power is high enough? ie provided that the anticipated coefficient is substantially lower than the standard error. Generally we aim for low VIFs but is there anything inherently wrong with having high values of this? I suppose it means that whilst the model will predict the response well within the factor space, making inferences about the underlying effects is more problematic.

I think that @statman you have conceptualised the problem in a similar way to me. For example the response at high and low A might be the same, hence the linear effect of A is negligible, and this is not affected by the level of B. However there is nonlinear behaviour such that the response at intermediate A is higher than at the extremes, and this deviation is dependent upon the level of B. The interaction profile would therefore look something like the attached picture (apologies for the rather hastily drawn example). In principle I do not see any reason why this could not be the case. Of course as @SDF1 correctly points out there could be a covariate factor that is determined by the combination of A*B but in this instance, based on knowledge of the system, I do not believe that to be true. I therefore come back to the question on whether, from an abstract statistical point of view, it is possible to generate a design where A*A*B has very low correlation with B, or whether this is not strictly possible and we have to take the approach of increasing the number of runs such that the design power is high enough that we can estimate the effect?