- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Why do intercept coefficients in generalized linear models depend on the design ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Why do intercept coefficients in generalized linear models depend on the design matrix
I've thought a lot about the intercept terms in glm. Logistic regression in particular. In standard linear regression we can estimate the intercept term without any knowledge of the design matrix. It's just the mean of the responses. I figured that principle would stay the same in other models. The principle is
- Once you know the responses and the link function, then you can determine the intercept term. It should be the same as running the glm dialog without any predictors (NULL model).
This is not the case. The intercepts are very close to the NULL model. I also get different intercept values if I change the design matrix. Maybe it's due to the fact that the coefficients are generated by a search algorithm. I also did the same thing for Poisson glm and found the same thing...the intercept is close to the NULL model but not the same.
Interestingly, if you run LASSO and continue to increase the penalty, the intercept does converge to (shrink toward) the NULL model. This result is independent of the design matrix.
I suppose it would be cool if you could simply calculate the intercept term from the responses and the link function prior to estimating the covariate coefficients. Would the model be better?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why do intercept coefficients in generalized linear models depend on the design matrix
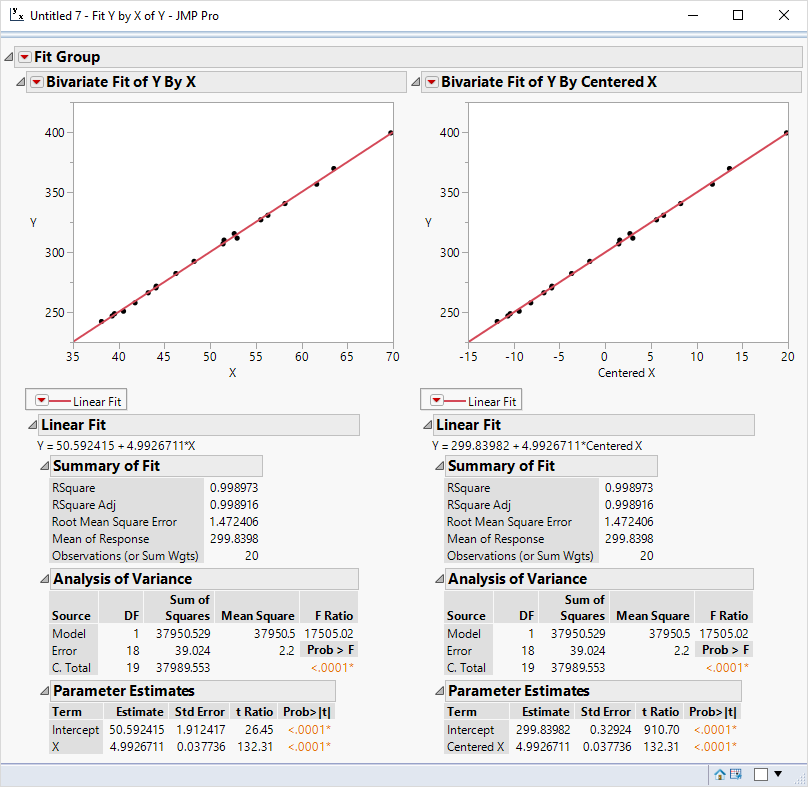
Just think about the y-intercept in this case of OLS regression where the first analysis uses X for the regressor and the second analysis uses X after centering:
So the intercept is not generally equal to the mean response but it will be if you center the predictor variables and use the identity link function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why do intercept coefficients in generalized linear models depend on the design matrix
The intercept (specifically, the y-intercept) is the constant term in the linear predictor (linear combination) used in ordinary least squares regression, generalized linear models, and generalized regression (JMP). It is generally the value of the linear predictor when all of the predictor variables are set to zero. It is not generally the mean response. That result depends on predictor values in the case of OLS regression. In the case of GLM, it also depends on the link function. If you want the intercept to be the mean response, then you must center your predictor variables and use the identity link.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why do intercept coefficients in generalized linear models depend on the design matrix
Just think about the y-intercept in this case of OLS regression where the first analysis uses X for the regressor and the second analysis uses X after centering:
So the intercept is not generally equal to the mean response but it will be if you center the predictor variables and use the identity link function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why do intercept coefficients in generalized linear models depend on the design matrix
Hello Mark,
I figured I'd get a quick and insightful reply from you. Thanks. I hadn't thought about the aspect of centering the X's. I was explicitly doing centering (and scale normalization) because I am applying LASSO to a logistic regression problem for feature selection. I can see that now if I don't center the design matrix I get a different answer. When it's centered, the intercept is almost exactly the link function applied to the mean response (fraction of positives). Very cool. The problem got me thinking about the picture I would present for LASSO shrinkage because the response space is now the corners of the unit cube. Add to that the optimal solution shrinks toward some point in the interior exactly equal to the mean response (times (1, 1, 1, ...)) as the penalty increases.
This whole thing led to a further question. One you might enjoy. There are some corners of the unit cube where a maximum likelihood solution doesn't exist. These are responses where JMP will tell us the coefficients are unstable because we have some linear combination of the columns of the design matrix that can perfectly classify the responses. The question I had was ...what is the maximum number of unstable corners as a function of the number of observations, N. Clearly the number must be less than 2^N because we rarely encounter unstable solutions (maybe always try linear classifier first to prevent this). The answer is pretty cool. It is related to the cake number sequence...it is Cake(N -1) in the case of 3 predictors. It gets really hard for more than 3 predictors.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why do intercept coefficients in generalized linear models depend on the design matrix
Thanks Mark,
The concept of centering the response is easy to understand in cases where the responses are numerical. Suppose we have a binary response such as {T, F} and I keep it in the uncoded form intentionally. There is no natural way to give meaning to centering the response. Even if we code it as {0, 1} and center the response we would generally end up with a vector of values between 0 and 1. This centered response is not in the set of realizable response vectors which must be a vector of 0's and 1's. So in this case the intercept term seems to be quite important to retain since it relates, through the link fuction, the fraction of 1's in the response. If there are the same number of T's and F's, then the intercept is 0...but not otherwise. So we can calculate the intercept from the response vector (kind of like centering the response) and then do lasso or whatever learning algorithm and just focus on the other columns.
So although I've been advised that centering binary responses is not a good idea, I think it's deeper than that. The intercept is important to carry with the model, even if it is not central to understanding the coefficients of the other predictors.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us