- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Why DF of pure error of LOF test change when terms are added or removed from...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Why DF of pure error of LOF test change when terms are added or removed from the model?
Hi JMPers,
I was modeling with fractional factorial design 2(7-4) with 3 center points.
When I change the terms in the model, DF of pure error in the LOF test also changes. (10 to 14)
In Minitab it doesn't change with the change of the model (same DF = 2 for 3 replicates of center points).
I think that DF of pure error is calculated from the number of pure replication so it cannot be changed while selecting different models.
Which result is right?
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
The first model that you ran in both JMP and MINITAB includes A, B, C, A*C, and BC. The second model is A and B with JMP but only B for MINITAB.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
Also, JMP does not split out the sum of squares for curvature and test it separately. It is just an omnibus LOF test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
You said that you used a 2^(7-4) regular fractional factorial design. This design is for the main effects model for 7 factors in 8 runs. You included 3 center points for a total of 11 runs. Your analysis shows that you have 19 runs so you either used a 2^(7-3) design or you replicated the 2^(7-4) design.
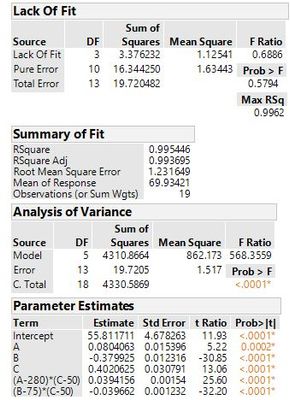
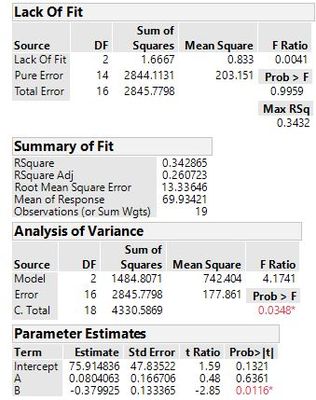
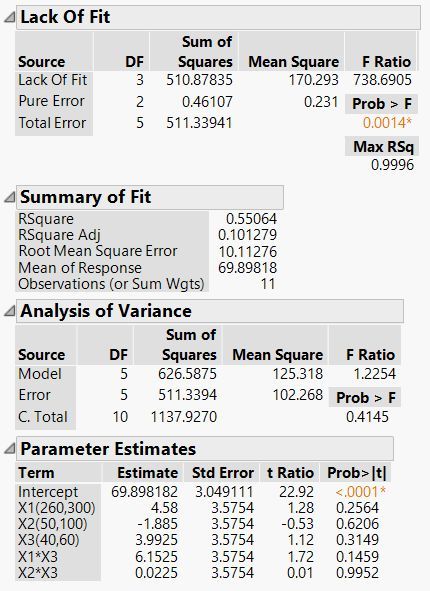
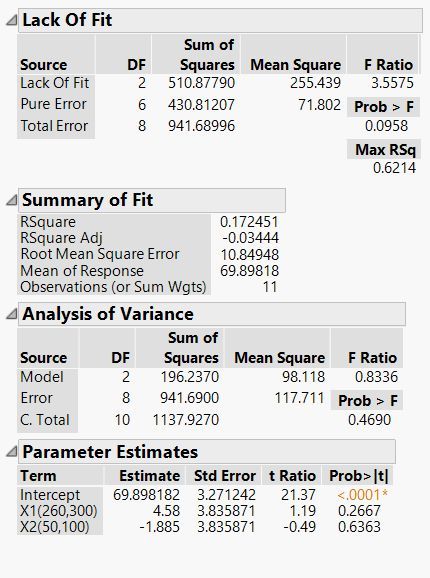
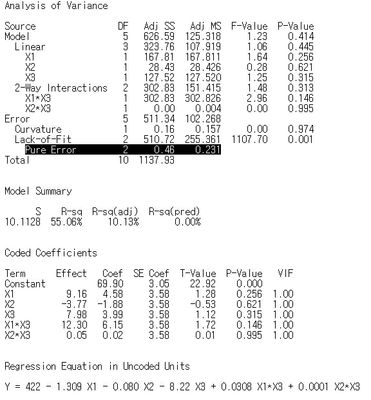
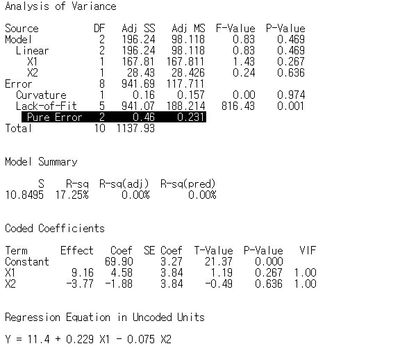
The DF for the LOF test are the same as the DF for the error SS in the AN0VA table. (Error DF = 13 in the first regression analysis.) The DF for the pure error are 1 less than the number of replicates. (Pure error DF = 1 DF for from each replicate FF design point + 2 DF from the replicate center points = 10.) The DF for the LOF is the difference between the two DF. (LOF DF = 13 - 10 = 3.) For the second case with just 2 main effects, the error DF = 16, pure error DF = 14, and LOF DF = 2.
As I said before, JMP is using all the DF not used by the model in an omnibus LOF test (any LOF). On the other hand, MINITAB is using more than one F-test for specific LOF components. They are different hypothesis tests so you can't expect them to be the same.
It is unfortunate, too, that JMP uses then opposite labeling for LOF terms than MINITAB. That is due to JMPs heritage from SAS. It adds to the initial confusion when comparing results across the two softwares.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
To be more specific about the claim by your source, that pure error SS is independent of the model, it depends on how the LOF is tested. The pure error and LOF DFs and SS are not independent of the model in the JMP test for LOF. The method presented in your source and (apparently) in MINITAB is model-independent.
The LOF test, however it is postulated, is a comparison of the model-dependent estimate of the random contribution (ANOVA error SS) to the model-independent estimate of the same (LOF pure error SS).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
The first model that you ran in both JMP and MINITAB includes A, B, C, A*C, and BC. The second model is A and B with JMP but only B for MINITAB.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
OK. I admit my mistake in getting the result in Minitab.
But my key question is how DF & SS of pure error in Lack-Of-Fit test are calculated and why they are different between softwares.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
You said that you used a 2^(7-4) regular fractional factorial design. This design is for the main effects model for 7 factors in 8 runs. You included 3 center points for a total of 11 runs. Your analysis shows that you have 19 runs so you either used a 2^(7-3) design or you replicated the 2^(7-4) design.
The DF for the LOF test are the same as the DF for the error SS in the AN0VA table. (Error DF = 13 in the first regression analysis.) The DF for the pure error are 1 less than the number of replicates. (Pure error DF = 1 DF for from each replicate FF design point + 2 DF from the replicate center points = 10.) The DF for the LOF is the difference between the two DF. (LOF DF = 13 - 10 = 3.) For the second case with just 2 main effects, the error DF = 16, pure error DF = 14, and LOF DF = 2.
As I said before, JMP is using all the DF not used by the model in an omnibus LOF test (any LOF). On the other hand, MINITAB is using more than one F-test for specific LOF components. They are different hypothesis tests so you can't expect them to be the same.
It is unfortunate, too, that JMP uses then opposite labeling for LOF terms than MINITAB. That is due to JMPs heritage from SAS. It adds to the initial confusion when comparing results across the two softwares.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
To be more specific about the claim by your source, that pure error SS is independent of the model, it depends on how the LOF is tested. The pure error and LOF DFs and SS are not independent of the model in the JMP test for LOF. The method presented in your source and (apparently) in MINITAB is model-independent.
The LOF test, however it is postulated, is a comparison of the model-dependent estimate of the random contribution (ANOVA error SS) to the model-independent estimate of the same (LOF pure error SS).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
As you pointed out, there are several mistakes in my analysis. Sorry for confusion.
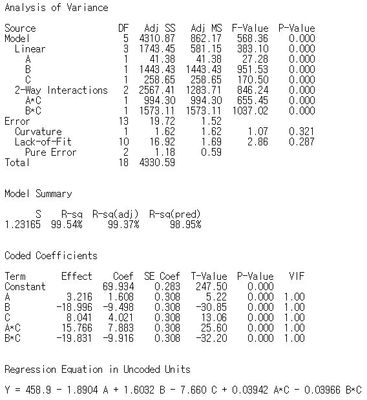
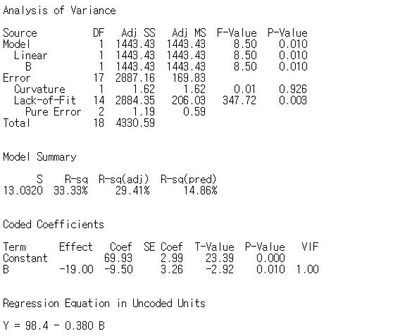
I posted correct analysis results.(2^(7-4) + 3 center points = 11 runs)
But the diffrence between softwares still exists.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
Also, JMP does not split out the sum of squares for curvature and test it separately. It is just an omnibus LOF test.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
We are planning to contain the result of the DOE analysis in the official report. (e.g. to Regulatory Affairs)
If the result of LOF test is different between softwares, how can I choose one? Are both results acceptable?
If statistical significance of two results is different? (p-value in JMP > 0.05, and p-value in Minitab < 0.05)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Why DF of pure error of LOF test change when terms are added or removed from the model?
The choice of the test is not based on agreement of the results or significance of these tests. Hypothesis tests are specific for the given alternative hypothesis, so the choice is based on the alternative hypothesis. JMP is testing any LOF. MINITAB is testing LOF differently.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us