- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Which test to evaluate the assumption of homegeneity of variances of residuals (...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Hi community,
In the residuals analysis, I evaluate normality and constant variance with the default graphs given in the regression analysis. However, I was wondering in which way I could test constant variance with a test that allow me to have sort of a p-value that make the situation more precise than looking at the graphs.
I am able to do it for normality, but not yet for the constance variance.
For example for the normality, I get the plot:
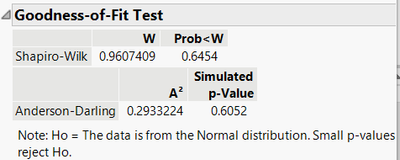
I can give some conclusions visually, but I also like to have a more precise description of the situation and therefore, I save the residuals and using the distribution platform (fit normal) I can get:
The shapiro-wilk test allow me to evaluate (in addition to the visual evaluation) the normality of my residuals.
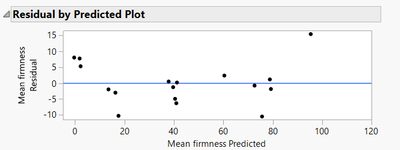
I am now looking to do something similar (doing a test) for the constance variance of the residuals in addition to the residual vs predicted plot (that I add here below)
I know that in the case of conducting an Anova in the "fit y by x" platform, there is the possibility of evaluating constance variance with "Lavene's test", but have not been able to do it in my case after plotting in this platform my saved residuals and saved predicted values.
Do you know if there is a way in addition to the plot to test constance variance for my residuals ?
Thanks for any help,
Julian
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
I think I found a nice tutorial from Professor Parris to do this:
Regression Diagnostics using JMP - Equality of Error Variance (youtube.com)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Did you notice this in the residual by predicted plot or in the residual normal quantile plot ?
Your residual by predicted plot shows a curvature pattern. This is a strong evidence that one of the assumption behind the use of linear regression is not respected (errors should be normally distributed with random pattern, see Regression Model Assumptions | Introduction to Statistics), and that you might be missing some effects in your model : quadratic effect(s) (or higher order terms), and/or any terms introducing curvature in the relationship between your response and the factors, like interaction terms.
See more in the related posts :
Interpretation related to response model (RSM)
How I can I know if linear model or non-linear regression model fit to my variables?
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
I think I found a nice tutorial from Professor Parris to do this:
Regression Diagnostics using JMP - Equality of Error Variance (youtube.com)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Aside from the requested test, your residual plot suggests lack of fit. Could there be a non-linear effect in the residuals?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Thank you @Mark_Bailey for your comment.
Did you notice this in the residual by predicted plot or in the residual normal quantile plot ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Did you notice this in the residual by predicted plot or in the residual normal quantile plot ?
Your residual by predicted plot shows a curvature pattern. This is a strong evidence that one of the assumption behind the use of linear regression is not respected (errors should be normally distributed with random pattern, see Regression Model Assumptions | Introduction to Statistics), and that you might be missing some effects in your model : quadratic effect(s) (or higher order terms), and/or any terms introducing curvature in the relationship between your response and the factors, like interaction terms.
See more in the related posts :
Interpretation related to response model (RSM)
How I can I know if linear model or non-linear regression model fit to my variables?
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which test to evaluate the assumption of homegeneity of variances of residuals (apart from residual vs predicted plot) ?
Thank you @Victor_G for your reply,
I actually did the verification of residuals and performed a box cox transformation which improved the situation. I cannot really add more terms since we had a rather simple case with not too many degrees of freedom.
However, your message allowed me to see the point in @Mark_Bailey comment. I was forgetting that interactions and quadratic terms bring that non-linearity to the model if added after verification of residuals. A silly oversight from my part : S
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us