- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Which one to define effect size: Logworth or Scaled Estimates ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Which one to define effect size: Logworth or Scaled Estimates ?
Hi Community,
I have a question concerning which criteria is more appropriate to determine the importance of the impact of a factor: is it the "logworth" (clearer visualization of p values) or is it the "scaled estimates" ?
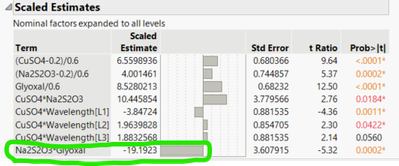
When working with one of the sample datas (Donev Mixture Data), I got these results for Logworth and for scaled estimates (images below):
Logworth:
Scaled Estimates:
You can see that in the first image, the one with the highest Logworth is "Glyoxal" and I would think this is the more impactful effect. However, if we look at the "scaled Estimates" in the second picture, it is rather the interaction Na2S2O3*Glyoxal that seems to have more impact.
Could you please help me understand this ? and what is really the part of my report to look at for saying which factor has more impact ?
Thank you,
Julian
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
Hi @Julianveda,
You are comparing two different and complementary informations, statistical and practical significance.
Statistical significance refers to the likelihood that an observed result or relationship between variables occurred by chance. In other words, it is a measure of how confident we can be that a relationship exists between two or more variables. In statistical analysis, this is typically assessed using a p-value (or logWorth, which is just calculated using -log transformation of the corresponding p-value), which is the probability of obtaining a result at least as extreme as the one observed, given that the null hypothesis (i.e., the hypothesis that there is no relationship between the variables) is true. If the p-value is below a certain threshold (e.g., 0.01, 0.05, or 0.1), the result is considered statistically significant, indicating that the observed relationship is unlikely to have occurred by chance and that the null hypothesis can be rejected. In the context of mixtures like in your example, traditional model selection techniques using p-values are not useful : due to multicollinearity between estimated effects (aliases between effects), standard errors of the estimates are quite large, resulting in misleading and distorted p-values. More infos in this discussion : https://community.jmp.com/t5/Discussions/Analysis-of-a-Mixture-DOE-with-stepwise-regression/m-p/6570...
Practical significance refers to the real-world importance or relevance of a statistical result. It is concerned with whether or not the observed relationship has any practical or meaningful implications. The practical significance is indicated by the size of the estimates : the bigger (in absolute value) for a term, the more important and the more influence has this term in the regression model of the response considered.
Note that statistical and practical significance may not always be closely related : a result can be statistically significant but practically insignificant, or the opposite situation. It is important to consider both significances when interpreting results.
I hope this first answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
Hi @Julianveda,
You are comparing two different and complementary informations, statistical and practical significance.
Statistical significance refers to the likelihood that an observed result or relationship between variables occurred by chance. In other words, it is a measure of how confident we can be that a relationship exists between two or more variables. In statistical analysis, this is typically assessed using a p-value (or logWorth, which is just calculated using -log transformation of the corresponding p-value), which is the probability of obtaining a result at least as extreme as the one observed, given that the null hypothesis (i.e., the hypothesis that there is no relationship between the variables) is true. If the p-value is below a certain threshold (e.g., 0.01, 0.05, or 0.1), the result is considered statistically significant, indicating that the observed relationship is unlikely to have occurred by chance and that the null hypothesis can be rejected. In the context of mixtures like in your example, traditional model selection techniques using p-values are not useful : due to multicollinearity between estimated effects (aliases between effects), standard errors of the estimates are quite large, resulting in misleading and distorted p-values. More infos in this discussion : https://community.jmp.com/t5/Discussions/Analysis-of-a-Mixture-DOE-with-stepwise-regression/m-p/6570...
Practical significance refers to the real-world importance or relevance of a statistical result. It is concerned with whether or not the observed relationship has any practical or meaningful implications. The practical significance is indicated by the size of the estimates : the bigger (in absolute value) for a term, the more important and the more influence has this term in the regression model of the response considered.
Note that statistical and practical significance may not always be closely related : a result can be statistically significant but practically insignificant, or the opposite situation. It is important to consider both significances when interpreting results.
I hope this first answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
Hello @Victor_G ,
Thank you very much for your answer. It has helped a lot to get things clearer :smiling_face_with_smiling_eyes: and at the sime time it has raised complementary questions:
- For the mixture doe, if p-values are not ideal, which could be the most appropriate criteria from the report to discard non statistically significant terms in the model ?
Is it better to remove one term at a time and observe evolution of AIC and/or RMSE as you mention in Solved: Re: Analysis of a Mixture DOE with stepwise regression - JMP User Community ? or also, selecting the model using backward selection as is discussed in the same thread ?
- In the practical significance, apart from the size of the effects in the “scaled estimates”, it is also important the domain knowledge right ? Let’s imagine I kept a quadratic term in the model and it actually preseted the highest effet in the “scaled estimates” table, but then (for any reason), we decided that term finally don’t make any sense in our domain. We can complete it discarder it despite its high importance in the estimates. Am I right ?
Best,
Julian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
Hi @Julianveda,
Glad that this first answer helped you.
Concerning your questions :
- For Mixtures DoE, I wouldn't rely on p-values for the reasons mentioned above (and in the other topic if I remember well).
I would start with the assumed complete model (this is why I would prefer Stepwise Backward Selection instead of Stepwise Forward Selection), and then refine the model if needed by comparing the RMSE levels of the different models, and/or using Maximum Likelihood estimation (available in Generalized Regression in JMP Pro) or an information criterion, like BIC/AICc, to determine a "right" number of terms that add information and predictivity without complexifying the model too much.
There are potentially many equivalently good models available, so using Domain Expertise as well as several selection/estimation methods can help sort out important terms and relevant models. - Domain Knowledge is always important, and at each step of DoE.
However, you have to remain cautious when adding or deleting terms in your model, as the reason you're doing this is to "help" statistical modeling with domain information (to sort out equally good but different models), not distort the statistical reality and results to your judgment and domain expertise. Also modeling is a dynamic process, adding or removing terms will change the estimates of the other terms as well, so some caution is really needed. DoE is a tool to test, verify, confirm hypotheses, but you can also learn new things opposite to what have been known before, perhaps because the experimental process was not rigorous enough to discover it before (like using One Factor At a Time Approach, or having sparse experimental results).
So I can't provide a definitive answer here to your question, however you can try different models, see how each model behave (residual analysis, actual vs. predicted, etc...) and test the models with new data. You should be able to rank the models by running validation points, corresponding to new treatments/factors combinations not seen before by the model or used in the design, and compare their results with the predictions. The model(s) with the best agreement on these new points may represent a closely good approximation of the physical system under study.
Hope these answers will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Which one to define effect size: Logworth or Scaled Estimates ?
Victor has done an excellent job of describing the different types of analysis: Practical and Quantitative. I would just provide a different point of view of the relative importance of each and add a third. Practical Significance is ALWAYS more important than statistical. After all, you control statistical significance by determining how the experiment will be run (e.g., inference space, what noise will change during the experiment and what noise will not). It isn't helpful to have a model that is statistically significant but is not useful in the real world. Recall the statistics of analysis are enumerative and developing a model for predictive purposes is analytical.
Deming (Deming, W. Edwards (1975), On Probability As a Basis For Action. The American Statistician, 29(4), 1975, p. 146-152) Use of data also requires understanding of the distinction between enumerative and analytic problems. “Analysis of variance, t-test, confidence intervals, and other statistical techniques taught in the books, however interesting, are inappropriate because they provide no basis for prediction and because they bury the information contained in the order of production. Most if not all computer packages for analysis of data, as they are called, provide flagrant examples of inefficiency.”
As Victor suggests, p-values are of little use for mixture designs. If you are running mixture designs, SME (domain knowledge) is critical. First determine, before running the experiment, what changes in the response are of practical significance.
Before running any quantitative analysis, plot the data. Particularly with mixtures, as the most important analysis is the mixture response surface. In theory, mixtures are an optimization strategy. This assumes you already know what should be in the mixture (through previous experimentation which includes processing factors). Statistical significance is no longer critical.
Practical>Graphical>Quantitative is the order of analysis.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us