What is the difference between paired comparison p-values in JMP and the "T-test" function in excel?

[#1]

Hi,

If there is anyone out there who can explain the difference between the p-values in JMP and the value calculated with the "T-test" function in excel, I would be very grateful.  I will give the following explanation to elucidate the quandary that I face.

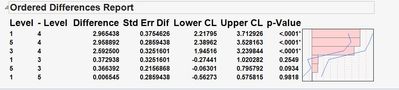
My experiment consisted of the mass of 82 different samples.  This sample set consisted of 4 separate groups (labeled 1,3,4,5) with each group consisting of 25 different samples.  When I read the "ordered difference report" from the XY graph measurement, I get the following p-values

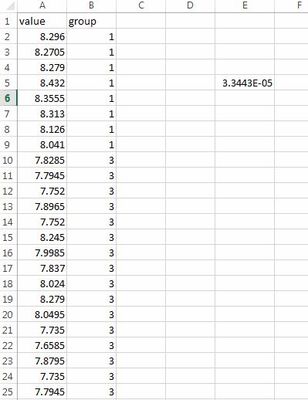
However, when I do the same test on the raw data in excel (formatted as the table below)

using the "T-test" function in excel with the following format "=TTEST(A2:A9,A10:A25,2,2)" (choosing a test between group #1 and group #3) the value I get is much different than the one I get in JMP (0.2549).  Can anybody give a reason what the difference might be?

Thanks,

Tei

[#2]

That depends partly on the options you selected in JMP.

See the doc and clarify which options you choose.

Compare Means

[#3]

Sorry for not specifying earlier... We used the "Each Pair, Student's T-test" choice.  However, I tried different tests and it didn't seem to make a tremendous difference...

Thanks,

Tei

[#4 · Accepted solution]

I am not sure what you got in Excel but it looks to me that one difference is that JMP will use a common estimate of the variablility based on all 5 groups while Excel is just estimating the variability from Groups 1 and 3.  This could make your p-values different.

[#5]

ToddS:  I believe you are correct. I have investigated this issue before and came to a similar conclusion.

Tei: If you run the same t-test in JMP on just the subset of data containing groups 1 and 3 you should be able to confirm that the p-values between Excel and JMP agree in this limiting case.

[#6]

Hi Guys,

I would like to conclusively determine which statistic to believe as it might tell us if something "(possibly) works" or "(probably) won't".  What statistic would you believe?  Is there any better way to determine a better way of answering this logical statement using the above example as a reference?

Thanks,

Tei

[#7]

Tei,

You should consider a different method other than t-test, which has its own limitations. I know Tukey is often considered superior for comparing means with more than 2 groups.