- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- What is the Adj. Power calculation in the Parameter Estimates telling me? Is th...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
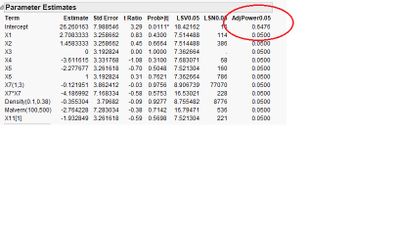
What is the Adj. Power calculation in the Parameter Estimates telling me? Is this the (1 - Beta) power at alpha = 0.05?
How do you interpret these power values? How can an intercept have a p
ower?
thanks for your help,
JoeH
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: What is the Adj. Power calculation in the Parameter Estimates telling me? Is this the (1 - Beta) power at alpha = 0.05?
Hi JoeH,
The model intercept, like any parameter, has uncertainty in its estimation - statistical power in estimating the intercept answers the question "what is the probability (given a random sample of size n from a population in which the intercept is some particular value different from 0) that the hypothesis test on the intercept would show the observed sample statistic is statistically significantly different from 0."
The adjusted power calculations you're referring to are the estimates of retrospective power for a given term; that is, given a new sample with an identical variability profile drawn from a population with parameters equal to the observed statistics, what is the probability that a particular term would be statistically significant. Retrospective power should be interpreted carefully, and not confused for prospective power. Consider this: a parameter with a p-value of exactly p=0.05 would have retrospective power = 0.50 (assuming a two-tailed test and alpha=0.05). That seemed odd to me at first, but if you draw the sampling distribution of the statistic given the alternative hypothesis being true with a value equal to the sample value observed, the center of this sampling distribution under the alternative is exactly at the criterion for rejecting the null hypothesis (which is true in definition -- a p-value == alpha means the parameter under consideration is exactly as far from 0 as the criterion for rejection itself). So, half of the sampling distribution under the alternative hypothesis is less than the criterion for rejection, and half is above the criterion for rejection, thus a random sample of that parameter from the sampling distribution under the alternative hypothesis has a 0.50 probability of exceeding the criterion.
The calculation of adjusted power there (while still a retrospective power calculation) takes into account some additional things. Here is the text from JMP help explaining the calculation:
"AdjPower0.05 is the adjusted power value. This number is an estimate of the probability that this test will be significant. Sample values from the current study are substituted for the parameter values typically used in a power calculation. The adjusted power calculation adjusts for bias that results from direct substitution of sample estimates into the formula for the non-centrality parameter (Wright and O’Brien, 1988)."
and the cautionary note from the help:
"Caution: The results provided by the LSV0.05, LSN, and AdjPower0.05 should not be used in prospective power analysis. They do not reflect the uncertainty inherent in a future study."
I hope this helps!
Julian
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us