Variance partitioning in a GLM

[#1]

Hi. I am wondering how to determine the portion of variance in the dependent variable that is explained by each independent variable in a GLM. I know this is doable in R, but would prefer to stick with JMP if possible. Thanks, Marthe

[#2]

You can use the Variability platform to do this:

Analyze==>Quality and Process==>Variability/Attribute Gauge Chart

[#3]

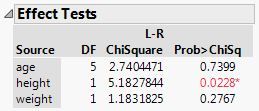
You might use the likelihood ratio chi square (L-R ChiSquare) presented in the Effect Tests report. This quantity would serve your purpose the same way as the sum of squares for each term would in ordinary least squares linear regression:

You might also use the Assess Variable Importance command in the red triangle menu for the Prediction Profiler (you have several choices of methods depending on the nature of your predictors):

(Thanks to my colleague, Di Michelson, for thinking of the profiler.)

[#4]

Thank you so much! This was very helpful.

[#5]

Hi Mark @markbailey,

How can the L-R ChiSquare quantities presented in the Effect Tests of a GLM in JMP be converted to the percentage of total variance explained? Can you be more specific? Is there a way to convert these values so that it is known what percentage of the variance is explained by each of the independent variables, and also, what percentage is left unexplained?

Thank you,

[#6]

I am not sure about the equivalent to the variance. We use sum of squares with a continuous response and negative log likelihood (-L) with a categorical response. For example, R square for a continuous response is the model SS divided by the corrected total SS. You can also look at the SS associated with the individual terms. For the categorical response, R square is the model -L divided by the reduced model -L.

I don't know if you can use the -L for individual terms to determine the contribution or if this quantity is what you mean by variance.