- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- TOST Acceptance criteria and Sample Size
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
TOST Acceptance criteria and Sample Size
Hello,
I'm analyzing historical data and need to find meaningful equivalence acceptance criteria between groups and calculate sample size for a new experiments. How can I set Practically equivalence acceptance criteria and I'm using the DOE Sample Size and Power calculator K means. Which prospective means should I enter.
Thank You
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
Of course you can set more stringent criteria for this test. This aspect of the TOST is not a statistical matter, though, unless you mean by "more stringent" that you require greater significance (lower alpha level) in the test.
The distribution of the historical data refers to individual outcomes. The TOST is a test of the mean of the population. The historical data could be used to estimate the mean and the standard deviation.
Use DOE > Design Diagnostics > Sample Size and Power > One Sample Mean. It turns out that sample size is the same as for TOST. The difference to detect is the difference between the mean and the criteria limit.
You have specifications so you could use them for your new criteria. You could determine a reasonable margin of safety. For example, in my example above, if I want a 50% margin, then I would set my criteria as y > 9.95 and y < 10.05. You don't need the distribution of historical data to set the criteria.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
The practically equivalent acceptance criteria are not statistical confidence bounds or limits. Like specifications, they are based on unacceptable performance or failure criteria. You might, for example, determine that a particular attribute of the material, part, or device must be within 0.1 of 10 or else it does not perform as claimed. The practically equivalent acceptance criteria are y > 9.9 and y < 10.1 in this case. So the answer to your question is that they come from specifications.
The equivalence test that you mention (TOST) is a pair of hypothesis tests where the acceptance criteria define the null. hypothesis:
H0: mean < 9.9 or mean > 10.1
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
Thank You,
I have historical values and all are within specification, but I would like to set equivalency acceptance criteria more stringent than specifications, to demonstrate for examples that two lots are practically equivalent. Can I set stringent equivalency acceptance criteria setting a rule from the distribution of historical data?
Also I need to set Sample size for the test from the Sample size calculator (Could I use Sample size calculator for a t-test and which prospective means do I enter in the calculator)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
Of course you can set more stringent criteria for this test. This aspect of the TOST is not a statistical matter, though, unless you mean by "more stringent" that you require greater significance (lower alpha level) in the test.
The distribution of the historical data refers to individual outcomes. The TOST is a test of the mean of the population. The historical data could be used to estimate the mean and the standard deviation.
Use DOE > Design Diagnostics > Sample Size and Power > One Sample Mean. It turns out that sample size is the same as for TOST. The difference to detect is the difference between the mean and the criteria limit.
You have specifications so you could use them for your new criteria. You could determine a reasonable margin of safety. For example, in my example above, if I want a 50% margin, then I would set my criteria as y > 9.95 and y < 10.05. You don't need the distribution of historical data to set the criteria.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
Ok many thanks,
DOE > Design Diagnostics > Sample Size and Power > One Sample Mean it also aks me for Std dev, is this from historical data?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
Exactly!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
I want to determine the sample size for a two sample equivalance test.
I would like alpha and beta to be 0.05. A practical difference is <-10 or >10. My standard deviation is 9.43.
How would I set this up using the one sample test sample size in jmp? Would you please be specific as to what I should enter in each field.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
*** NOTE 1: I updated my original reply because it did not address the two sample test for equivalence. ***
*** NOTE 2: This method is for a hypothesized difference. It should NOT be used for calculating the sample size for equivalence.
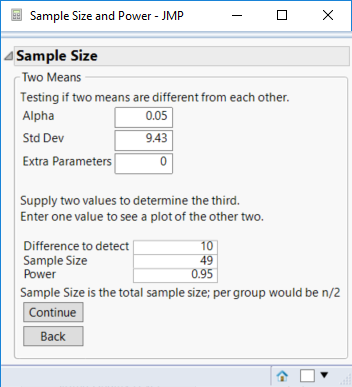
I believe that you determine the sample size for a TOST of equivalence exactly the same as a two sample test of the mean. I don't have the paper handy (it is an old one) but we get lucky here and they are the same. Select DOE > Design Diagnostics > Sample Size and Power. Click Two Sample Mean and enter your values as seen below, then click Continue to obtain the sample size (49, or 25 for each group, in this case).
I will investigate further when I get a chance to determine if there is another way or if I was wrong that you can use this method.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
I am trying to do a two sided equivalence test. When I ran it through Minitab I got 24. I also used the folowing formula = (2*((-1.96 -1.6449)^2)*9.43^2 )/10^2 in Excel and got 23.11.
Please advise how I can obtain this from JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: TOST Acceptance criteria and Sample Size
I don't think that anyone should use the method I showed most recently for a two sample test. That result is for the hypothesized difference, not equivalence. MINITAB and your hand calculation provide the sample size for one population assuming a balanced design. I implemented the computation as a JMP script:
alpha = 0.05;
beta = 1 - 0.95;
delta = 10;
sigma = 9.43;
ratio = 1;
z alpha = normal quantile( 1 - alpha );
z beta = normal quantile( 1 - beta );
n = Ceiling( ((1 + 1/ratio) * sigma^2 * (z alpha + z beta)^2) / (delta^2) );For this case of 95% confidence, 95% power, a standard deviation of 9.43, and a significant difference of 10, I get N1 = N2 = 20.
The result is for one sample. The sample size for the other population is the ratio times the first sample size. The ratio is 1 for a balanced design.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us