- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Suggestion on experimental design strategy for chemical synthesis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Suggestion on experimental design strategy for chemical synthesis
Happy Sunday, a wonderful community of JMP!
I will likely have to design and run a set or sequential experiments to maximize the yield of chemical synthesis.
Someone in our group ran this chemical reaction in the past. However, my manager wants me to repeat this reaction to better understand the relationship between reaction conditions and yield. Based on the historical data, there are three takeaways.
1. Total calcium concentration is very important.
2. The ratio of ammonia to potassium in the reaction impact the yield but at lesser extent.
3. Total ammonia concentration might have some impact on reaction but hard to estimate degree (or size) of impact based on the historical data.
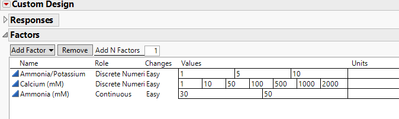
Therefore, I set up the three factors I want to investigate: 1) calcium concentration, 2) the ratio of ammonia to potassium, and 3) Ammonia concentration.
Here I included 7 different levels of calcium concentrations as it changes the yield across a broad concentration range of calcium. We also want to have three discrete ratios of ammonia and potassium. Then I also want to investigate whether ammonia concentration impact the yield.
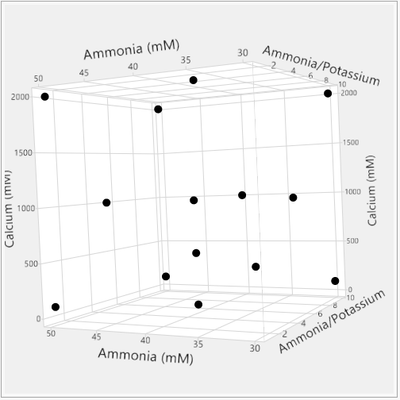
Below is what JMP suggested, and I am quite satisfied as: 1) it suggested 14 runs within the resource limit. 2) it efficiently fills up the design space.
However, as indicated earlier, it is hard to gauge if ammonia concentration has any impact on the yield purely based on the historical data. I am tempted to run a small pilot study to see whether ammonia concentration has any impact. For instance, I run three reaction conditions where the calcium concentration and the ratio of ammonia to potassium concentrations are fixed, and the ammonia concentration is varied (30~50 mM).
If ammonia ends up not having a significant impact on yield, I would be able to build more thorough RSM with only two factors (calcium concentration and the ratio of ammonia to potassium). However, at the same time, I would be missing an opportunity to investigate the potential impact of ammonia on yield at different concentrations of calcium and the ratio of ammonia to potassium (it is more like one factor at a time + DOE).
I would like to get any opinions from more experienced JMP users on how to approach this kind of problems.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Hi @BJK_JerseyBoy,
It's great you already have historical data, as it may provide a good baseline and comparison to the new experiments you'll create.
Concerning your factors, I don't understand why you set the Ammonia/Potassium ratio factor as discrete numeric ? You can set up this factor as numerical continuous, and add a quadratic term in the model panel so that the resulting design will include a middle level. The Calcium concentration factor does cover a wide range, but again, you're not forced to use a discrete numeric factor to cover a broad range of levels : specifying a more complex model with higher order terms (set as "Necessary" or "If Possible" to not augment the required run size), and/or using a log scale for this factor, since it covers very different orders of magnitude for the concentration (so instead of having 1/10/50/100/500/1000/2000 you would have 0/2,3/3,9/4,6/6,2/6,9/7,6 with a log-scale, which would enable to cover more homogeneously the different concentrations magnitudes compared to the original scale with a numerical continuous factor).
Concerning your questions about ammonia concentration, why not broadening the factor range which seems very small compared to the other factors ? Ammonia may not have been detected previously as a significant factor because the range in which this factor varies is not big and may not enable to detect significant differences between high and low levels. Expanding its range could provide you more information about its influence in your system (if technically possible).
One option could be to use this initial set of historical data, and use the platform Augment Designs in order to create a DoE that can be built on this set and still assess/confirm if these first observations seem plausible. When augmenting a design, you can still change the factors ranges if needed, to explore a broader (or narrower) experimental space. If you think this option might be interesting to consider, make sure the option "Group new runs into separate block" is checked, so that you can estimate a possible fixed or random effect due to a variability change between the historical data / new data from Augment DoE.
Another option could be to set up a "new" DoE like you do, in order to build a model understanding of the system and compare it with runs from production/historical data, to see if the model enables you to understand/predict results in the narrow production space.
As @Florian_Vogt mentioned, it's important to remember that DoE supports a sequential experimentation approach, so you can start with a big experimental space and only a very simple model, and then adjust the ranges and add more complexity (if needed !) to refine your understanding and/or build a predictive model.
I hope this answer may help you and give you "food for thought" :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Hi @BJK_JerseyBoy,
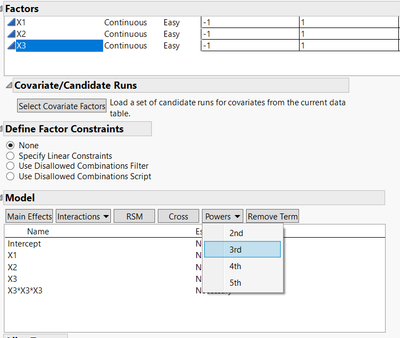
Yes, in order for the Custom Design to provide more than 2 levels for any numeric continuous factor, you have to include higher order terms in the model, like quadratic effects (3 levels), cubic effects (4 levels), ...
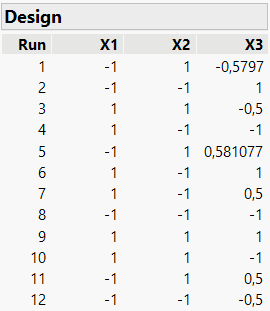
To do this, you can select your factor and click in the model panel on "Powers" and choose the order relevant to the number of levels you would like (example here for 4 levels with cubic power terms in the model) :
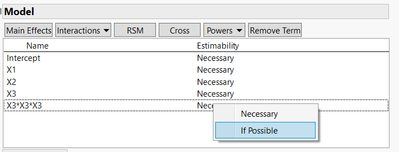
Note that you can change estimability of this/these terms to "If possible" to save some runs (click on the estimability of the term, and you'll have the option displayed) :
Adding this term in the model will create more levels on this factor in the design (4 levels: -1 / -0,5 / 0,5 / 1)
I hope this answer will help you setup your design.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Hi @BJK_JerseyBoy ,
there will likely be many with relevant experience and some ideas and suggestions to help you along.
Until then, maybe this article gives you some helpful information: The sequential nature of DoE
Have a good week,
Florian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Hi @BJK_JerseyBoy,
It's great you already have historical data, as it may provide a good baseline and comparison to the new experiments you'll create.
Concerning your factors, I don't understand why you set the Ammonia/Potassium ratio factor as discrete numeric ? You can set up this factor as numerical continuous, and add a quadratic term in the model panel so that the resulting design will include a middle level. The Calcium concentration factor does cover a wide range, but again, you're not forced to use a discrete numeric factor to cover a broad range of levels : specifying a more complex model with higher order terms (set as "Necessary" or "If Possible" to not augment the required run size), and/or using a log scale for this factor, since it covers very different orders of magnitude for the concentration (so instead of having 1/10/50/100/500/1000/2000 you would have 0/2,3/3,9/4,6/6,2/6,9/7,6 with a log-scale, which would enable to cover more homogeneously the different concentrations magnitudes compared to the original scale with a numerical continuous factor).
Concerning your questions about ammonia concentration, why not broadening the factor range which seems very small compared to the other factors ? Ammonia may not have been detected previously as a significant factor because the range in which this factor varies is not big and may not enable to detect significant differences between high and low levels. Expanding its range could provide you more information about its influence in your system (if technically possible).
One option could be to use this initial set of historical data, and use the platform Augment Designs in order to create a DoE that can be built on this set and still assess/confirm if these first observations seem plausible. When augmenting a design, you can still change the factors ranges if needed, to explore a broader (or narrower) experimental space. If you think this option might be interesting to consider, make sure the option "Group new runs into separate block" is checked, so that you can estimate a possible fixed or random effect due to a variability change between the historical data / new data from Augment DoE.
Another option could be to set up a "new" DoE like you do, in order to build a model understanding of the system and compare it with runs from production/historical data, to see if the model enables you to understand/predict results in the narrow production space.
As @Florian_Vogt mentioned, it's important to remember that DoE supports a sequential experimentation approach, so you can start with a big experimental space and only a very simple model, and then adjust the ranges and add more complexity (if needed !) to refine your understanding and/or build a predictive model.
I hope this answer may help you and give you "food for thought" :)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Agree with Victor. I would avoid discrete numeric unless there was a "dial" that made it impossible to make it continuous.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Here are some of my thoughts and questions. Victor gives some great feedback so I am adding to the menu (food for thought)! What is the ultimate objective of your study? Is it to pick a winner or to actually understand the mechanisms at work? What questions are you trying to answer? Do you want to explain the variation in the historical data set or develop a useful prediction model?
"However, my manager wants me to repeat this reaction to better understand the relationship between reaction conditions and yield."
Reaction conditions seems to me to include some other variables beyond just the 3 listed (calcium, ammonia and potassium). What about temperature, rate of change in temp., time, geometry of the container, agitation, etc.) As well as contaminants, purity of the chemicals, measurement errors of the chemicals, order of addition, etc. How do you measure yield? Have you studied the measurement system? From the historical data, is there any way to estimate consistency (do you know the time series?)?
Regarding factors: What is your hypothesized model you are trying to get insight into?
1. Calcium. Why is this discrete numeric (vs. continuous)? Why are you testing at 7 levels? This will bias the effects in the experiment to calcium. Do you really need to estimate a 6th order effect? (And you will get some extremely complex interactions). It seems you already know this is important, so is the question how important is it in comparison to the other factors in your study? Does it interact with other factors?
2. Ratio of ammonia to potassium. Agreed with question of factor type(Victor). Since you are experimenting on Ammonia, seems like this is really just amount of potassium? (Levels could be set with ratios in mind). Is this actually a mixture of ammonia and potassium (perhaps a mixture design)? Does the ratio depend on ammonia concentration?
Look at the dots on your experiment. Do they seem to be balanced throughout the design space? It appears biased to me.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Thank you @Victor_G and @statman for sharing insightful thoughts and providing suggestions.
I learn a lot from you guys from here as well as sporadic linkedin posts.
@Victor_G _ I will definitely convert discrete numeric to continuous factor. For calcium concentration, I love the idea of changing the numbers to log scale. However, I did not understand what you meant of "you're not forced to use a discrete numeric factor to cover a broad range of levels : specifying a more complex model with higher order terms (set as "Necessary" or "If Possible" to not augment the required run size)"
I picked 7 different levels of calcium concentraitons in the initial design as I know calcium concentration affect the yield at wide range. If I change calcium concentration from discrete numeric to continuos factor, custome design will likely pick low, middle, and high points in the design space. I know I can do sequential design (augment the design) to find the optimal chemical reaction. However, based on the historical data it might be hard to know which direction to go if I only have three levels of calcium concentrations. Is there a way to include one or two more levels of calcium cocentrations without having to do discrete numeric.
Ammonia concentration is experimentally bound from 30 -50 mM. We know that it will produce different by product outside of these ranges. As you pointed out, since the concentration range of ammonia is narrow, I was not sure if it would have any impact on the yield.
@statman Yes! There are more than three variables in the chemical reaciton. However, they are not considered to be changed. Another word, they have to be used as they are and reaction occurs at ambient temperature and pressure. Unfortuantely, I cannot gauge the consistency of this reaction as there is no replicates in the historical data.
Ammonia to potassium ratio is fixed, therefore, if I change the ammonia concentration, potassium concentration changes accordingly.
Thanks again for sharing insightful thoughts. Based on you guys' suggestion, I am thinking to change the ratio from discrete numeric to continuous factor. Is there anyway to have calcium concentration as continous factor but set 4-5 levels without having to use discrete numeric?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Suggestion on experimental design strategy for chemical synthesis
Hi @BJK_JerseyBoy,
Yes, in order for the Custom Design to provide more than 2 levels for any numeric continuous factor, you have to include higher order terms in the model, like quadratic effects (3 levels), cubic effects (4 levels), ...
To do this, you can select your factor and click in the model panel on "Powers" and choose the order relevant to the number of levels you would like (example here for 4 levels with cubic power terms in the model) :
Note that you can change estimability of this/these terms to "If possible" to save some runs (click on the estimability of the term, and you'll have the option displayed) :
Adding this term in the model will create more levels on this factor in the design (4 levels: -1 / -0,5 / 0,5 / 1)
I hope this answer will help you setup your design.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us