- JMP User Community
- :
- Discussions
- :
- Statistical test for algorithm comparison - JMP Pro
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Statistical test for algorithm comparison - JMP Pro
Hello,
I want to test the efficiency of two different algorithms.
I have two random samples from the same population. On one sample, I run Algorithm X; on another sample, I run Algorithm Y. There are 30 records in each. The variable type is continuous.
Which statistics test I can do to find out the best algorithm and what parameters I should be comparing?
Kindly let me know if more details are needed.
Thanks
Nick
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical test for algorithm comparison - JMP Pro
Statistical inference is helpful when observing the entire population is impossible. The population is not defined in your post. Statistical inference assesses the uncertainty in the estimation of a parameter due to sampling from the population. Compare the two algorithms based on a measure of efficiencies such as processing time or processing steps using the same sample of data. This case is a paired comparison that can use the paired t-test on the continuous outcome of each algorithm.
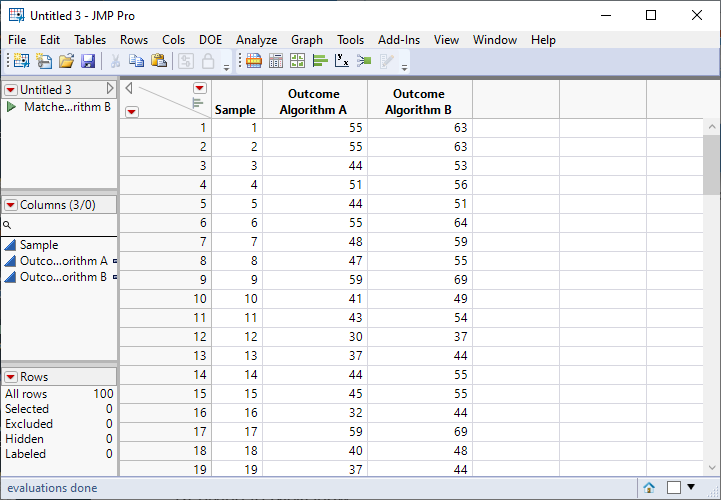
Your data might look like this table:
I mocked up some data. There are 100 samples of data from the same population. The samples could be from resampling or bootstrapping. The outcome is the number of seconds to complete the algorithm.
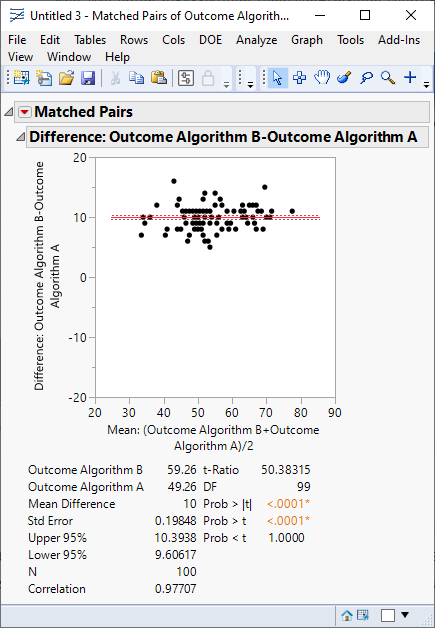
You can analyze these results using Analyze > Specialized Modeling > Matched Pairs.
This example shows a statistically significant difference between the two algorithms of about 10 seconds.
I attached my mock-up for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical test for algorithm comparison - JMP Pro
I have lots of questions and very few answers without alot more information.
1. What characteristic would you like to use to evaluate 'efficiency'?
2. What characteristic would you like to use to evaluate 'best'? If whatever your characteristic for 'best' is, how much does the results have to vary before you declare one is 'best'?
3. There are numerous population 'parameters' that one can evaluate from 'random samples' from said population. Are you attempting to estimate these parameters? If so, by what method? Confidence intervals, tolerance intervals, something else? Is there a time series component to the data or decisions at hand?
4. Is this an academic exercise or one that has practical decisions behind it? If the latter, please articulate more of the practical problem, sampling method (truly random...or something else), and the actual decisions at hand.
5. What do you know about measurement noise/variation with respect to the processes in play?
6. I hope you have examined the data graphically BEFORE doing any numeric analysis. There may be outliers, suspicious observations, or other features in the sample data sets that make any one specific numeric analysis approach more problematic than alternative approaches.
I've probably not touched on everything but the above is a start?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical test for algorithm comparison - JMP Pro
Statistical inference is helpful when observing the entire population is impossible. The population is not defined in your post. Statistical inference assesses the uncertainty in the estimation of a parameter due to sampling from the population. Compare the two algorithms based on a measure of efficiencies such as processing time or processing steps using the same sample of data. This case is a paired comparison that can use the paired t-test on the continuous outcome of each algorithm.
Your data might look like this table:
I mocked up some data. There are 100 samples of data from the same population. The samples could be from resampling or bootstrapping. The outcome is the number of seconds to complete the algorithm.
You can analyze these results using Analyze > Specialized Modeling > Matched Pairs.
This example shows a statistically significant difference between the two algorithms of about 10 seconds.
I attached my mock-up for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical test for algorithm comparison - JMP Pro
Thanks a lot Mark.
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us