- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Statistical Significance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Statistical Significance
Hi,
I have the following information only:
I have Failure Rates (FR) from two sets of data. The experiment set has 4 fails out of 2500 (FR:0.16%) samples and the control set has 34 fails out of 35000 samples (FR:0.097%). Due to such a big difference in the sample size, is there a way JMP can help to determine if these two FRs are statistocally similar or different?
Thanks.
Ravi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
Hi @RaviK,
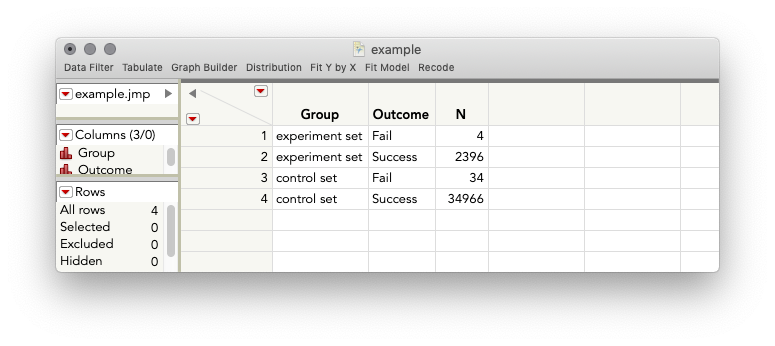
There are a few ways you could approach this, but perhaps the most straightforward is a Chi-Square Test of Independence, a type of contingency analysis. This test is appropriate because what you have are two categorical variables, a grouping variable, and a categorical outcome (success or fail), and you are interested in whether the observed proportions of the categorical outcome for your two groups provide evidence that the process generating the outcomes differs between the groups. You can obtain this test using Analyze > Fit Y by X. But first, you'll first need your data entered in a particular way (also attached):
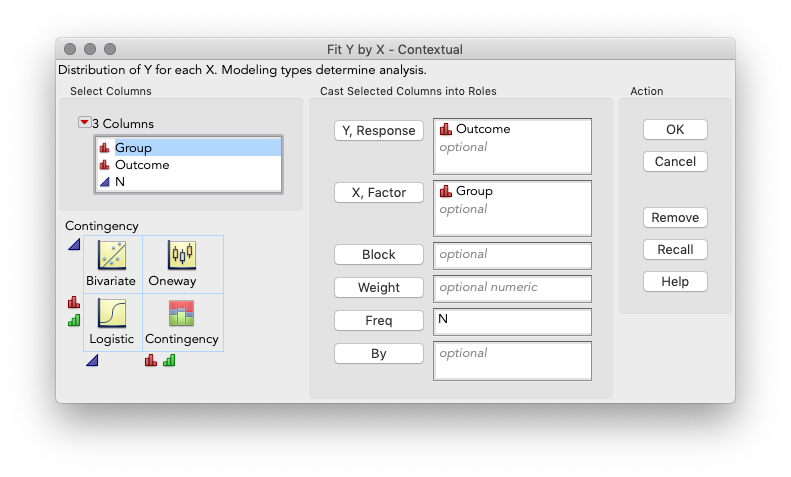
What I've done is taken the numbers you provided me and made columns for Group, Outcome, and N, the number of observations in each. For the number of successes, I simply took the total you gave minus the failures. Next, we run Analyze > Fit Y by X:
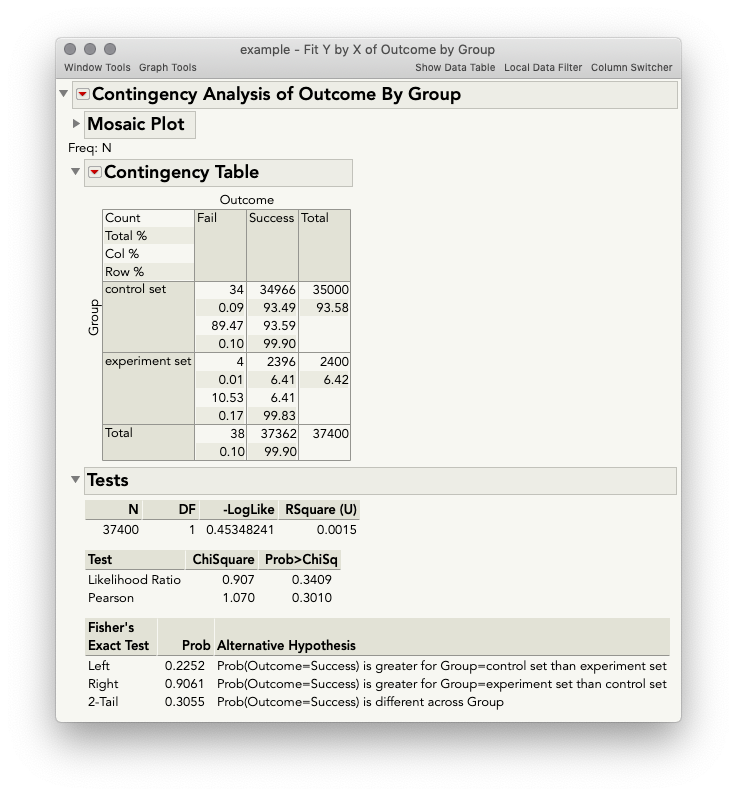
Here I've cast Outcome in the Y role, Group to the X, and N as the Freq, or frequency of occurrence. When we hit OK, we get the output below (I've hidden the mosaic plot since your observed frequencies of fail are so low that the plot is not helpful).
Our p-value of interest is the Likelihood ratio, or Pearson (classical Chi-Square test of independence), both of which are around p = ~0.30, indicating that if there isn't any true difference in the experimental and control group processes, a difference in the proportion of failures you observed in these sample data (or a difference more extreme) would occur about 30% of the time when taking samples of the sizes you had. In other words, not very convincing evidence that there is a true difference in these sets. Given what appears to be a large difference in the proportion of failures this may be surprising; but, given the low failure count overall, it's relatively easy to observe differences in the proportions of this magnitude or greater simply by chance (which is what this statistical significance test is telling us directly).
I hope this helps!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
Don't know if it helps understanding, but here's some JSL that gets the pValue directly through simulation:
NamesDefaultToHere(1);
n1 = 2500; // Size of sample one
nf1 = 4; // Number of failures in sample one
n2 = 35000; // Size of sample two
nf2 = 34; // Number of failures in sample two
n = n1 + n2;
nf = nf1 + nf2;
nSim = 10000; // Number of simulations
np1 = J(nSim, 1, .); // Vector to hold the number of passes counted in sample one
// Randomly allocate nf failures to n units
for(s=1, s<=nSim, s++,
result$ = J(n, 1, 1); // All n units pass initially
result$[randomIndex(n, nf)] = 0; // Simulate nf failures at random
np1$ = VSum(result$[1::n1]); // Count the nummber of passes in sample one
np1[s] = np1$; // Store this result
);
// Now evaluate how extreme the observed number of passes, (n1 - nf1), is in relation to the
// reference distribution constructed under the null hypothesis of random allocation of
// failures to samples
np1Observed = n1 - nf1;
pValue = NRow(Loc(np1 <= np1Observed)) / nSim;
Print("Estimated pValue is "||Char(Round(pValue, 3)));- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
Thanks Ian.
Ravi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
Thanks Julian. It was useful indeed.
Could I also use "Hypothesis Test for two Proportions"?
Ravi
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Statistical Significance
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us