- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Significant Two Sample Test for Proportion but not significant Chi-square
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Significant Two Sample Test for Proportion but not significant Chi-square
Hi all
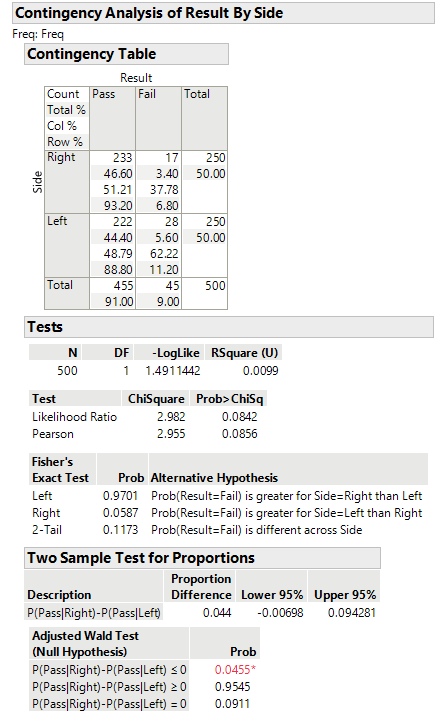
I'm working with data from some pass-fail testing, where a difference in performance has been observed for some samples grouped into left and right. I'm trying to analyse whether this is a real difference or rather variation due to statistical variance. I'm doing this by using the Contingency analysis (Fit X by Y) framework in JMP.
The issue is that I'm a bit confused by the results, which are shown below. Assuming a confidence of 95%, the Chi-Square test shows that the ratio of passed and failed devices does not appear to be dependent on if they are left or right samples.
Now if i also perform a Two Sample Test for Proportions to test if the probability off passes for right side samples will be lower than or equal to the number of left side passes, i find that i can reject this hypothesis, implying that passes for right side samples are higher.
I know that these two tests test different type of hypothesis, but it seems to me that these to conclusions contradict each other.
Finally, looking at the two sample test I find that the confidence interval goes from -0.7% to 9.4% for the difference P(pass|right)-P(pass|left), which surprising to me appear to contradict the conclusion drawn for the two sample test just above. Shouldn't all values in this interval be above or equal to zero?
All comments and suggestions are welcome to help me understand all these great tools. :)
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant Two Sample Test for Proportion but not significant Chi-square
The two sample test shows a confidence interval which contains zero - this is consistent with the hypothesis test because it is the two sided test you want to compare it to. In both cases, subject to a 5% level of confidence, you cannot reject the hypothesis of equality. The difference between the chi-squared results and the Wald test will require someone with deeper statistical knowledge than mine. But I will note that the numbers don't differ that much, and I'd also note that the chi-square test has a number of alternative results (again, which require deeper knowledge than mine to explain the differences). I would not expect identical numerical results, but I see that they are qualitatively quite similar.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant Two Sample Test for Proportion but not significant Chi-square
Thank you Dale.
But would you say that it is correct to conclude that the left side type devices are significantly more prone to failing based on the results shown then?
Following this logic:
HA: P(Pass|Right) - P(Pass|Left) > 0
H0: P(Pass|Right) - P(Pass|Left) ≤ 0
Significance: 0.0455
Given a confidence level of 95% we can reject the null and accept the alternative hypothesis, that it is more likely for a right type device to pass than a left type device. Vice versa it is more likely for a left type device to fail than a right type device
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Significant Two Sample Test for Proportion but not significant Chi-square
That is a technically correct conclusion, but I prefer to avoid dichotomous thinking. The uncertainty tends to get lost - I think the confidence interval is a bit more useful in that it shows how uncertain the conclusion is from this particular sample. Also, while we are generally more interested in the direction of the difference (rather than testing whether the difference is actually zero), it is traditional to view 2 sided hypothesis tests (if you must do a test at all). In this case, the result looks fairly marginal and I would not base any real decisions on these results without specifying more clearly the costs involved with potential errors (Type 1 and 2 errors).
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us