- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Setting up a DOE with a transformed Factor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Setting up a DOE with a transformed Factor
Hi -
I am setting up a simple 2 factor response surface design. We know from prior experimentation, that X2 is best used for model building in transformed units, which is in this case LN X2. The question is, would it be better to use for DESIGN GENERATION the LN X2, instead of going with the physical unit of X2? By using physical units and do a LN transform on X2 for analysis with the responses obtained, the design of the 2 factor RSM is "losing symmetry". For illustration, I added a pic. Again: does this "loss of symmetry" has any impact on the analysis?
There is no impact on VIF ... but is there anything else I need to consider?
Additional comment: I noticed that, when adding constraints to the design, the induced (slight) factor correlation between X1 and X2 due to applying 2 constraints, is further increasing, when the design is set up and run in physical units and being afterwards LN transformed for the response analysis.
Thanks for your comments.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting up a DOE with a transformed Factor
Hi @Uwe_Weber,
If you're sure that transformed units have a "physical sense" (practical meaning) and that you'll always be using these transformed units instead of the original units, I would also consider using transformed units directly from the start (design generation) to ensure better coverage of the design space. If you'll always use transformed units for the factors in the responses modeling, the estimation of parameters may be slightly more accurate by generating the design on transformed units ; for example, the polynomial effects X1² and X2² are best estimated with points at min, max and middle levels of the factor range. In your screenshot, you'll lose this "balance"/optimality if not designing from the start with transformed units, resulting in slightly less precise parameters estimation.
This type of approach can be seen in litterature for non-uniform space filling design, in order to cover the experimental space with specific distribution, focussing on specific area or with factors having large orders of magnitude. See "Non-uniform space filling (NUSF) designs" by Lu Lu, Christine M. Anderson-Cook & Towfiq Ahmed, https://doi.org/10.1080/00224065.2020.1727801
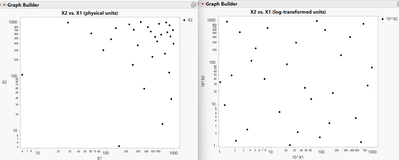
For factors having large orders of magnitude, here is a typical example where log-transformed factors could be interesting in order to have good coverage of the design space even in the presence of high order magnitude of variation for 3 factors (each with range from 1 to 1000). On the left, a Space-Filling design with 30 runs and with natural units (axes are logarithmic scales). You can see that for this design, you have a large majority of runs with high values, and very few covering small values for X1 and X2 (and no runs with factors values below 100 !). When designing your DoE with log-transformed factors (range 0 to 3 instead of 1 to 1000 in natural units), image on the right, you see a better coverage of the runs for high and low values for factors X1 and X2.
The only "inconvenient" might be in the interpretation of the results that may be a little more complex and less straightforward, but you can prepare some formula for your factors (from original units to transformed units), do your modeling on transformed units, and "expand intermediate formula" in the Prediction Profiler to display the prediction results in original units.
Hope this answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting up a DOE with a transformed Factor
Hi @Uwe_Weber,
If you're sure that transformed units have a "physical sense" (practical meaning) and that you'll always be using these transformed units instead of the original units, I would also consider using transformed units directly from the start (design generation) to ensure better coverage of the design space. If you'll always use transformed units for the factors in the responses modeling, the estimation of parameters may be slightly more accurate by generating the design on transformed units ; for example, the polynomial effects X1² and X2² are best estimated with points at min, max and middle levels of the factor range. In your screenshot, you'll lose this "balance"/optimality if not designing from the start with transformed units, resulting in slightly less precise parameters estimation.
This type of approach can be seen in litterature for non-uniform space filling design, in order to cover the experimental space with specific distribution, focussing on specific area or with factors having large orders of magnitude. See "Non-uniform space filling (NUSF) designs" by Lu Lu, Christine M. Anderson-Cook & Towfiq Ahmed, https://doi.org/10.1080/00224065.2020.1727801
For factors having large orders of magnitude, here is a typical example where log-transformed factors could be interesting in order to have good coverage of the design space even in the presence of high order magnitude of variation for 3 factors (each with range from 1 to 1000). On the left, a Space-Filling design with 30 runs and with natural units (axes are logarithmic scales). You can see that for this design, you have a large majority of runs with high values, and very few covering small values for X1 and X2 (and no runs with factors values below 100 !). When designing your DoE with log-transformed factors (range 0 to 3 instead of 1 to 1000 in natural units), image on the right, you see a better coverage of the runs for high and low values for factors X1 and X2.
The only "inconvenient" might be in the interpretation of the results that may be a little more complex and less straightforward, but you can prepare some formula for your factors (from original units to transformed units), do your modeling on transformed units, and "expand intermediate formula" in the Prediction Profiler to display the prediction results in original units.
Hope this answer may help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Setting up a DOE with a transformed Factor
Thanks Victor ... that was very helpful.
Cheers,
Uwe
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us