- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Repeated measures survival analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Repeated measures survival analysis
Dear Members of the community,
I would like to analysis the duration of a process performed 8 repeated times with 30 computers and five different operating systems. as in the attached data file. this data is also censored, when duration was longer than 180 seconds it was just deemed to be a failure.
the main aim is to test the following hypotheses:
1) is there a difference between operating systems?
2) is there a difference between attempts?
3) is there an interaction between operating systems and attempts?
My main concern is whether the recurrence analysis platform is the most suitable and how to define the variables correctly.
I have attempted to tackle this with a repeated measures full factorial mixed model but couldn't find a satisfying transformation that would give me reasonably behaving residuals. (script in the data table)
would be thankful for any ideas,
Ron
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Quick response is that we don't have the tool to address the situation yet: repeated measure with censoring.
If we can ignore the fact that the measurements are repeated on individual computers, we can still get something out of the data.
The following are what I did: a Graph Builder report to look at the data; a Parametric Survival report to fit some models; a Life Distribution report to inspect residuals; and finally a Graph Builder report to look at the data and predicted values side by side.
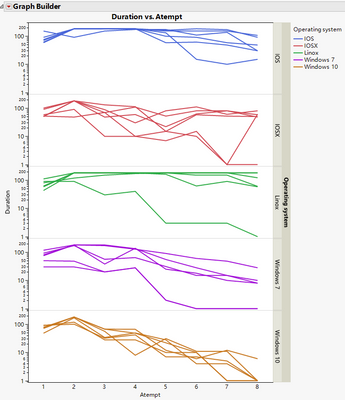
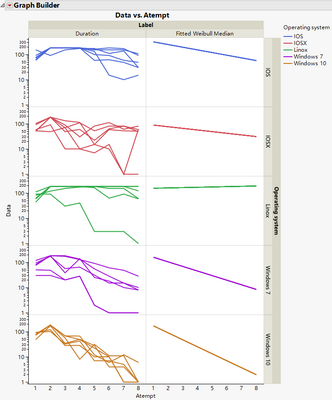
First is a plot of the data: Duration vs. Atempt, grouped by OS, overlaid by Computer ID. So by OS, they all present a downward trend. Windows10 machines do stay tightly. Other machines stay more or less stay together by OS. IOS and Linox have relatively more right censored observations. So a preliminary answer to your interest is that Atempt and OS matter.
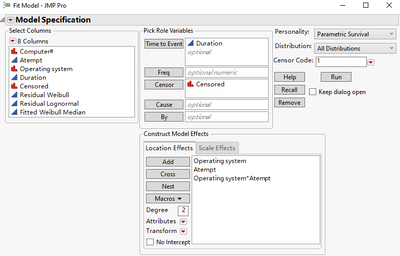
Now I attempt to fit a model. Based on what I see in the plot, a Parametric Survival analysis should be appropriate. So the setup is to see whether I can fit a distribution to Duration, while the location parameter of the distribution is a linear function of the effects. The Scale Effect tab is empty, so I am not considering the scale parameter of the distribution is a linear function of some effects, but it can be tried later to see whether it matters.
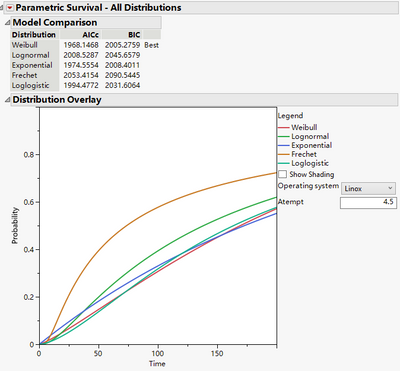
The report says Weibull is the best fit, followed by Lognormal. Also individual distribution reports show effects are significant.
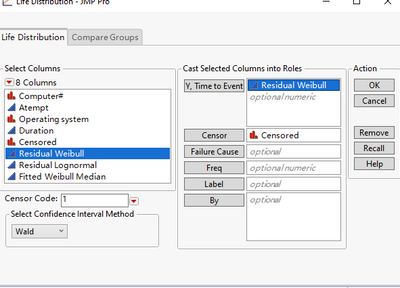
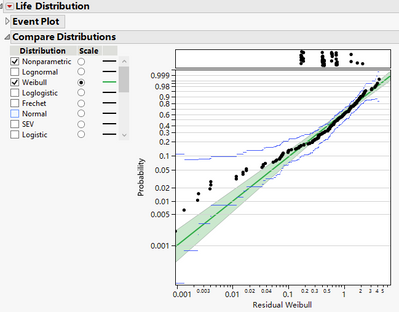
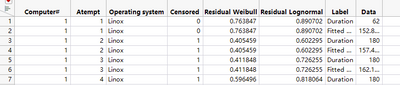
I then save the residuals from Weibull and Lognormal results back into the table. The use Life Distribution to look at them. Notice when put Residual into the Y role in Life Distribution, the Censor column needs to go to the Censor role, like what's in the following screenshot.
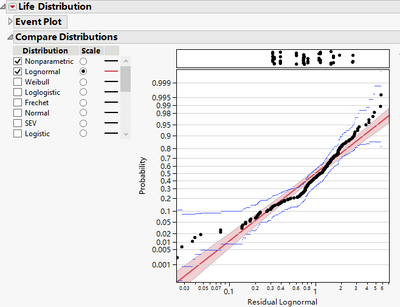
Analyze the Lognormal residuals similarly and compare the two reports. Weibull does seems to be a better fit, because linearization seems to better fit Weibull. Lognormal has a more significant kink.
Then from the Parametric Survival report, I save "Quantile Formula" from the Weibull result. When it prompts for "probability", enter 0.5, for the median. Now the data table has an extra column, and I name it "Fitted Weibull Median". Then I stack "Duration" and "Fitted Weibull Median", and get a new data table, so for every observation in the original table, I have a corresponding predicted median.
Use Graph Builder to put data and predicted values side by side, the model looks pretty reasonable.
The above may not be the only plausible way to fit the data, but I am not going to exhaust them here. I attach the updated data table and the stacked data table as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Heck! Authentication failure. Lost my long reply. Restart. Kind of forget what I said...
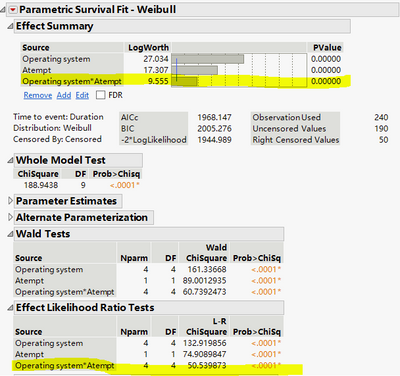
The Weibull result shows the interaction is significant. See the highlighted places in this screenshot:
Notice the results from Parametric Survival are conditional distributions given factors. So it is rather different from OLS, from which comparisons, which are responses typically, can be done by looking at the parameter estimates.
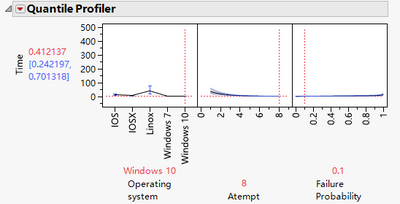
For here, I suggest using either Probability or Quantile profiles in the Weibull result. You need to turn them on in the Weibull result menu. Take Quantile profiler as an example; see next screenshot.
I fix Failure Probability = 0.1, and change OS and Atempt. So for this particular screenshot, the y-axis read off says: for Windows 10 machines, at 8th Atempt, 10% of machines will finish the operation under 0.412137 unit of the time measure. Then change OS or Atempt, or both to compare different scenarios. Fixing probability is the key to keep comparisons clear. Given OS and Atempt, the curve in the third frame, quantile curve, always go up.
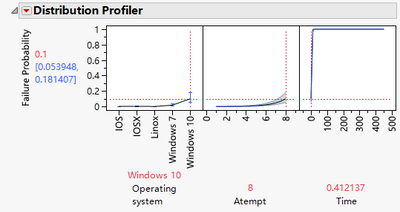
Similarly, for Probability profiler like the following. It reads: by 0.412137 time unit, at 8th Atempt, 10% of Windows 10 machines should complete the operation. Then compare scenarios by changing OS and Atempt or both. Also fixing Time is the key to keep comparisons clear. The last curve, distribution curve, always go up.
Cox model looks similar. One can also think of it as fitting distributions with covariates. Notice the distributions are semi-parametric here. And the model imposes an extra assumption. The reports look similar too. But the interpretations about the model and parameter estimates are quite different. I will only go that route if (1) none of the distributions in Parametric Survival fit the data, (2) there is an assumption that hazard functions are proportional. I believe that Cox model will complicate the situation for this data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Quick response is that we don't have the tool to address the situation yet: repeated measure with censoring.
If we can ignore the fact that the measurements are repeated on individual computers, we can still get something out of the data.
The following are what I did: a Graph Builder report to look at the data; a Parametric Survival report to fit some models; a Life Distribution report to inspect residuals; and finally a Graph Builder report to look at the data and predicted values side by side.
First is a plot of the data: Duration vs. Atempt, grouped by OS, overlaid by Computer ID. So by OS, they all present a downward trend. Windows10 machines do stay tightly. Other machines stay more or less stay together by OS. IOS and Linox have relatively more right censored observations. So a preliminary answer to your interest is that Atempt and OS matter.
Now I attempt to fit a model. Based on what I see in the plot, a Parametric Survival analysis should be appropriate. So the setup is to see whether I can fit a distribution to Duration, while the location parameter of the distribution is a linear function of the effects. The Scale Effect tab is empty, so I am not considering the scale parameter of the distribution is a linear function of some effects, but it can be tried later to see whether it matters.
The report says Weibull is the best fit, followed by Lognormal. Also individual distribution reports show effects are significant.
I then save the residuals from Weibull and Lognormal results back into the table. The use Life Distribution to look at them. Notice when put Residual into the Y role in Life Distribution, the Censor column needs to go to the Censor role, like what's in the following screenshot.
Analyze the Lognormal residuals similarly and compare the two reports. Weibull does seems to be a better fit, because linearization seems to better fit Weibull. Lognormal has a more significant kink.
Then from the Parametric Survival report, I save "Quantile Formula" from the Weibull result. When it prompts for "probability", enter 0.5, for the median. Now the data table has an extra column, and I name it "Fitted Weibull Median". Then I stack "Duration" and "Fitted Weibull Median", and get a new data table, so for every observation in the original table, I have a corresponding predicted median.
Use Graph Builder to put data and predicted values side by side, the model looks pretty reasonable.
The above may not be the only plausible way to fit the data, but I am not going to exhaust them here. I attach the updated data table and the stacked data table as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Thank you very much @peng_liu, your answer moves me forward quite a few steps.
If this was a linear model, we could use a post hoc test on the interaction term to explicitly compare each combination of attempt and Operating system with every other one. how would you go about making all these comparisons in this case?
for this reason, the solution i came up with was also ignoring the repeated aspect and running a Cox proportional hazard model for each attempt. There, the comparison between each operating system was explicit (but limited to the attempt)
Thank you once again.
Ron
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Heck! Authentication failure. Lost my long reply. Restart. Kind of forget what I said...
The Weibull result shows the interaction is significant. See the highlighted places in this screenshot:
Notice the results from Parametric Survival are conditional distributions given factors. So it is rather different from OLS, from which comparisons, which are responses typically, can be done by looking at the parameter estimates.
For here, I suggest using either Probability or Quantile profiles in the Weibull result. You need to turn them on in the Weibull result menu. Take Quantile profiler as an example; see next screenshot.
I fix Failure Probability = 0.1, and change OS and Atempt. So for this particular screenshot, the y-axis read off says: for Windows 10 machines, at 8th Atempt, 10% of machines will finish the operation under 0.412137 unit of the time measure. Then change OS or Atempt, or both to compare different scenarios. Fixing probability is the key to keep comparisons clear. Given OS and Atempt, the curve in the third frame, quantile curve, always go up.
Similarly, for Probability profiler like the following. It reads: by 0.412137 time unit, at 8th Atempt, 10% of Windows 10 machines should complete the operation. Then compare scenarios by changing OS and Atempt or both. Also fixing Time is the key to keep comparisons clear. The last curve, distribution curve, always go up.
Cox model looks similar. One can also think of it as fitting distributions with covariates. Notice the distributions are semi-parametric here. And the model imposes an extra assumption. The reports look similar too. But the interpretations about the model and parameter estimates are quite different. I will only go that route if (1) none of the distributions in Parametric Survival fit the data, (2) there is an assumption that hazard functions are proportional. I believe that Cox model will complicate the situation for this data.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Repeated measures survival analysis
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us