- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Reference line from axis to specific value
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Reference line from axis to specific value
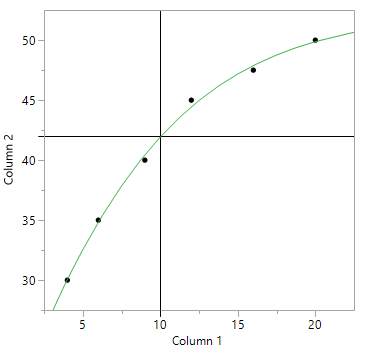
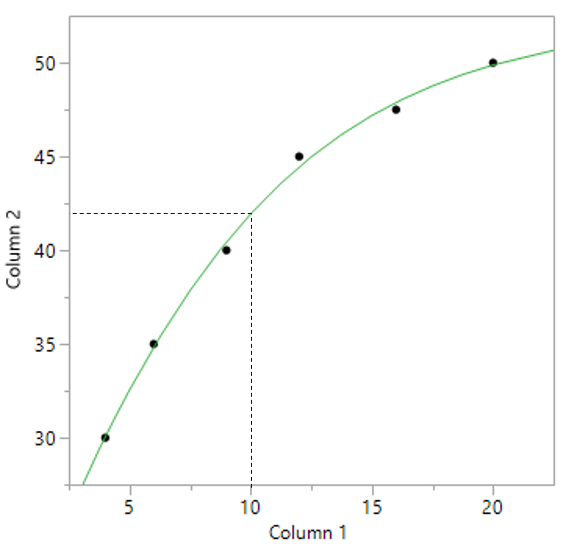
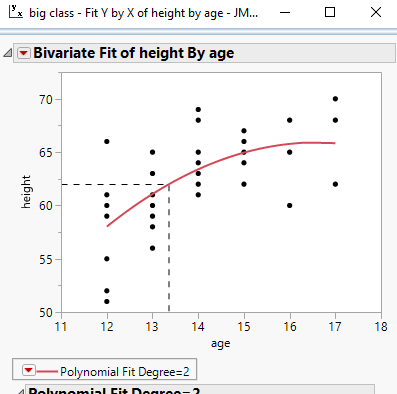
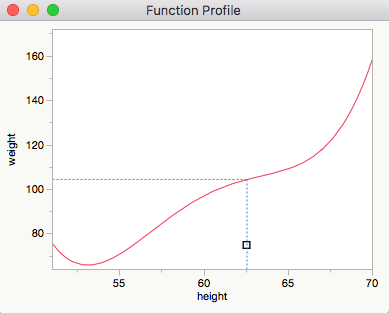
I am trying to script a graph that shows the predicted value on the y-axis from some specified value on the x-axis on a soft curve. I have managed to pull out the prediction formula and obtain the relevant values to define reference lines. However to communicate this effectively i would like the reference lines to stop at the curve and preferable to be dashed. The above image is as far as I have been able to go with jsl scripting. Below is where I would like to end up.
Thanks!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
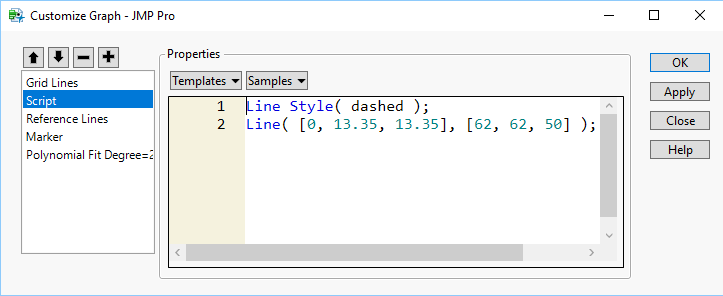
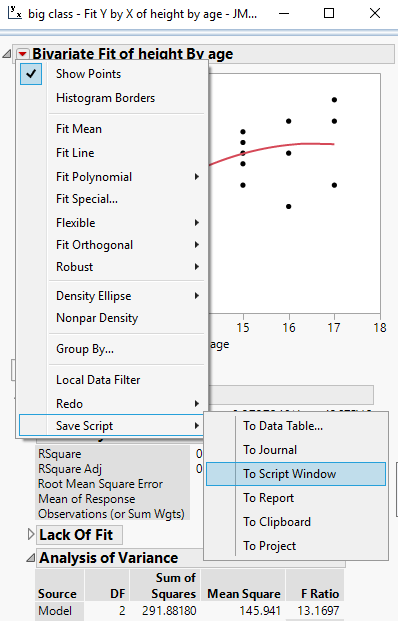
Adding to @MikeD_Anderson, the method that I have found easiest to develope the code for adding graphics to a chart in a platform, is to right click on the graph in question, and select "Custom". This allows one to modify and add to the graph in real time. I then simply click on th "+" and add a new segment
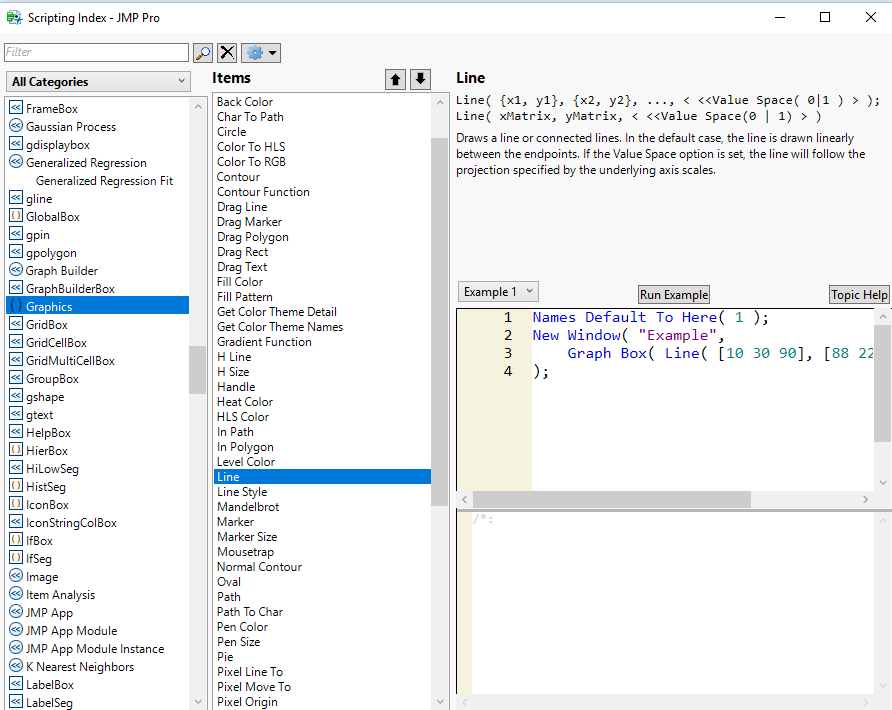
Using the Templates or Samples, or using the Scripting Editor's "Graphics Category"
one can play with the display until one has what they want.
You can go to the red triangle and Save the Script
Which will give you a sample script that you can then modify to make the script generic
Names Default To Here( 1 );
dt = Open( "$SAMPLE_DATA\big class.jmp" );
Bivariate(
Y( :height ),
X( :age ),
Fit Polynomial( 2, {Line Color( {213, 72, 87} )} ),
SendToReport(
Dispatch(
{},
"Bivar Plot",
FrameBox,
{Add Graphics Script(
2,
Description( "Script" ),
Line Style( dashed );
Line( [0, 13.35, 13.35], [62, 62, 50] );
), Grid Line Order( 1 ), Reference Line Order( 3 )}
)
)
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
Instead of using two reference lines from the axes, try drawing a rectangle in the graph box using a graphics script:
Names Default To Here( 1 );
New Window( "Example",
Graph Box(
// line color
Pen Color( "Green" );
// line width
Pen Size( 2 );
// line style (dashed)
Line Style (2);
Fill Color( "Red" );
// filled rectangle
Rect( 15, 75, 65, 55, 1 );
// unfilled rectangle (reference lines)
Rect( -1, 80, 70, -1 );
)
);M
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
Adding to @MikeD_Anderson, the method that I have found easiest to develope the code for adding graphics to a chart in a platform, is to right click on the graph in question, and select "Custom". This allows one to modify and add to the graph in real time. I then simply click on th "+" and add a new segment
Using the Templates or Samples, or using the Scripting Editor's "Graphics Category"
one can play with the display until one has what they want.
You can go to the red triangle and Save the Script
Which will give you a sample script that you can then modify to make the script generic
Names Default To Here( 1 );
dt = Open( "$SAMPLE_DATA\big class.jmp" );
Bivariate(
Y( :height ),
X( :age ),
Fit Polynomial( 2, {Line Color( {213, 72, 87} )} ),
SendToReport(
Dispatch(
{},
"Bivar Plot",
FrameBox,
{Add Graphics Script(
2,
Description( "Script" ),
Line Style( dashed );
Line( [0, 13.35, 13.35], [62, 62, 50] );
), Grid Line Order( 1 ), Reference Line Order( 3 )}
)
)
);
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
The code below should allow you to dynamically profile any saved formula column that involves only one input. In the case of 'Big Class' and a quartic model, it gives:
It's more or less untested.
NamesDefaultToHere(1);
// Function to find leaves in formula that are columns in the table
// See: https://community.jmp.com/blogs/Uncharted/2015/04/03/head-arg-recurse-formula"
// Thanks to Craige Hales
findColumns =
Function( {frm, cols},
{h = Head( frm ), n = N Arg( frm ), i, result = {}}, // local variables
If( n == 0, // head node has no children, it is a leaf
If( Contains( cols, Name Expr( h ) ), // is the leaf in the list of columns?
Insert Into( result, Name Expr( h ) ); // yes -> add to result
)
,
For( i = 1, i <= n, i++, // not a leaf, get children's results
Insert Into( result, Recurse( Arg( frm, i ), cols ) )
)
);
result; // return the result
);
// Open a table to play with, and add a formula column to it
dt = Open("$SAMPLE_DATA/Big Class.jmp");
fCol = dt << New Column( "Predicted weight",
Formula(-127 + 4 * :height),
Set Property("Predicting", {:weight, Creator( "Bivariate" ), Model Name( "Polynomial Fit Degree=3" )})
);
// Recover the required information
f = fCol << getFormula;
xColList = findColumns(NameExpr(f), dt << getColumnNames);
yCol = fCol << getProperty("Predicting");
yCol = yCol[1];
// Subsequent code will only work with one x Column
xCol = Expr(xColList[1]);
for(c=1, c<=NItems(xColList), c++, Print(c); if(xColList[c] != xCol, Print("Only one x Column allowed."); Beep(); Throw()));
// Reparameterise the formula for later use in the 'GraphBox()'
SubstituteInto(f, xCol, Expr(x));
// Set the initial 'VLine()' value to the mean of the x values
xVals = xCol << getValues;
x = Mean(xVals);
// Get 'reasonable' ranges for the axes
xMin = Min(xVals);
xMax = Max(xVals);
yMin = Min(yCol << getValues);
yMax = Max(yCol << getValues);
// Get the names of the columns involved
xColName = xCol << getName;
yColName = yCol << getName;
// Plot the graph
NewWindow("Function Profile",
gb = GraphBox("Simple Profiler", XScale(xMin, xMax), YScale(yMin, yMax), XName(xColName), yName(yColName),
// Plot the function
PenColor("Red"); YFunction(f, x);
// Handle to drag the 'VLine()' and update display
Handle(x, yMin + (yMax-yMin)/10, gb << reShow, Empty());
// Get the function value for the current x value
yy = Eval(Substitute(NameExpr(f), Expr(x), x));
// Plot the lines at the new places
PenColor("Blue"); LineStyle("Dotted");
VLine(x, yMin, yy);
HLine(xMin, x, yy);
);
);- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
This look really cool but is probably also a bit above my current level of understanding. I will try to work my way trough your example and will hopefully learn quite a bit in the process!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Reference line from axis to specific value
Thanks a lot, this was just what I was looking for!
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us