- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Query on generating DOE with four (2-level) variables and analyzign 2 variables ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hello:
I have 4, 2-level variables and was planning to do a full factorial DOR run without replicate.
So 16 runs.
Instead of analyzing the result for four variables, what if I analyze only two variables at a time, this will give me total six DOE to analyze within the same set of 16 experiments but each with 4 replicates now.
Variables: A, B, C, D
instead of analyzing ABCD together, what if I analyze AB, AC, AD, BC, BD, CD.
This way I can see what factors and interactions are significant.
I believe DOE analyzer does the same, but than why it is always suggested to have more replicates?
Am I missing something or is my understanding flawed some where.
Your help is highly appreciated.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hi @VarunK,
There are several questions in your post, so I will try my best to answer step-by-step.
About the use of full factorial design and what to expect from it :
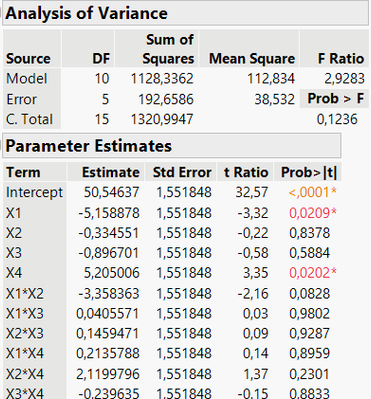
If you're planning to do a full factorial design on 4 continous factors with 2 levels with 16 runs, this means you assume your apriori full model will contain the intercept, the 4 main effects (for each factors) and the 6 interactions between 2 factors. In total, you have 11 terms to estimate, so you still have 5 degree of freedom left to assess the error : Analysis of Variance
I would recommend to start with the full model first, as it is your apriori assumed model so it may provide you a better overview of the relevance and influence of the different terms, instead of repeating the model fitting for a lot of different combinations without any prior knowledge (this would require a longer time, and you might get confused by different or conflicting models).
Of course, depending on your results, this full model may not be the most appropriate or relevant one, and there might not be one single model that may answer your needs.
Also if one (or several) factor(s) and its associated higher order terms (interaction effect) have no influence on the model, the runs corresponding to the estimation of these effects can be projected into the lower dimensional space, making them look like replicates. This is called the projection property of factorial designs, and the reason (with the sparsity of effects principle) why screening designs/fractional factorial designs can be very powerful and flexible. Several links are available on internet if you want to know more : Classical Designs-Fractional Fractorial Designs Rev1.pdf (afit.edu)
Projection Properties of Factorial Designs for Factor Screening | SpringerLink
And I also did a post on LinkedIn to explain intuitively how it works through a comparison with shadowgraphy : https://www.linkedin.com/posts/victorguiller_designofexperiments-statistics-dataanalytics-activity-7...
Adding replicates is a good technique to improve the estimation of the parameters/coefficients, but they can greatly increase the experimental budget. To provide a greater flexibility, and depending on the platform used, you can either use replicate (full replication of the design) or replicate runs (replication of a certain number of runs). For more info about this replication difference and the benefits of replicates, see https://community.jmp.com/t5/Discussions/Doe-and-replications/m-p/565296/highlight/true#M77731
About the way to analyze your DoE :
Depending on your objective(s), you may have different paths to models evaluation and selection :
- Explainative model : In an explainative mode, you're more focussed on the terms that do have some influence on the response(s), so you might evaluate the need to include the different terms based on statistical significance (with the help of p-values and a predefined threshold for it like 0.05) and practical significance (size of the estimates, selection based on domain expertise). R², R² adjusted (and the difference between the two, which needs to be minimized) might be good metrics to understand how much variation is explained by the identified terms, and select relevant model(s) to explain your system under study.
- Predictive model : In a predictive mode, you're more focussed on the terms that help you minimize prediction errors, so you might evaluate the need to include the different terms based on how this improve the predictive performances, through the visualizations of actual vs. predictive plot, and size of the errors (residuals plot). RMSE might be a good metric to assess which model(s) have the best predictive performances (goal is to minimize RMSE).
You might also be interested by a combination of the two parts, so different metrics could be used to help you evaluate and select model's, like information criteria (AICc, BIC) that help find a compromise between predictive performances of the model and its complexity. To evaluate and select a model based on these criteria, the lower the better. You might also use maximum likelihood which is similar but does not include a penalty for the complexity of the model.
As you can see, there might be several ways to evaluate and select the most relevant model(s).
I hope this answer will help you have an overview about what to do try next for your use case.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hi @VarunK,
There are several questions in your post, so I will try my best to answer step-by-step.
About the use of full factorial design and what to expect from it :
If you're planning to do a full factorial design on 4 continous factors with 2 levels with 16 runs, this means you assume your apriori full model will contain the intercept, the 4 main effects (for each factors) and the 6 interactions between 2 factors. In total, you have 11 terms to estimate, so you still have 5 degree of freedom left to assess the error : Analysis of Variance
I would recommend to start with the full model first, as it is your apriori assumed model so it may provide you a better overview of the relevance and influence of the different terms, instead of repeating the model fitting for a lot of different combinations without any prior knowledge (this would require a longer time, and you might get confused by different or conflicting models).
Of course, depending on your results, this full model may not be the most appropriate or relevant one, and there might not be one single model that may answer your needs.
Also if one (or several) factor(s) and its associated higher order terms (interaction effect) have no influence on the model, the runs corresponding to the estimation of these effects can be projected into the lower dimensional space, making them look like replicates. This is called the projection property of factorial designs, and the reason (with the sparsity of effects principle) why screening designs/fractional factorial designs can be very powerful and flexible. Several links are available on internet if you want to know more : Classical Designs-Fractional Fractorial Designs Rev1.pdf (afit.edu)
Projection Properties of Factorial Designs for Factor Screening | SpringerLink
And I also did a post on LinkedIn to explain intuitively how it works through a comparison with shadowgraphy : https://www.linkedin.com/posts/victorguiller_designofexperiments-statistics-dataanalytics-activity-7...
Adding replicates is a good technique to improve the estimation of the parameters/coefficients, but they can greatly increase the experimental budget. To provide a greater flexibility, and depending on the platform used, you can either use replicate (full replication of the design) or replicate runs (replication of a certain number of runs). For more info about this replication difference and the benefits of replicates, see https://community.jmp.com/t5/Discussions/Doe-and-replications/m-p/565296/highlight/true#M77731
About the way to analyze your DoE :
Depending on your objective(s), you may have different paths to models evaluation and selection :
- Explainative model : In an explainative mode, you're more focussed on the terms that do have some influence on the response(s), so you might evaluate the need to include the different terms based on statistical significance (with the help of p-values and a predefined threshold for it like 0.05) and practical significance (size of the estimates, selection based on domain expertise). R², R² adjusted (and the difference between the two, which needs to be minimized) might be good metrics to understand how much variation is explained by the identified terms, and select relevant model(s) to explain your system under study.
- Predictive model : In a predictive mode, you're more focussed on the terms that help you minimize prediction errors, so you might evaluate the need to include the different terms based on how this improve the predictive performances, through the visualizations of actual vs. predictive plot, and size of the errors (residuals plot). RMSE might be a good metric to assess which model(s) have the best predictive performances (goal is to minimize RMSE).
You might also be interested by a combination of the two parts, so different metrics could be used to help you evaluate and select model's, like information criteria (AICc, BIC) that help find a compromise between predictive performances of the model and its complexity. To evaluate and select a model based on these criteria, the lower the better. You might also use maximum likelihood which is similar but does not include a penalty for the complexity of the model.
As you can see, there might be several ways to evaluate and select the most relevant model(s).
I hope this answer will help you have an overview about what to do try next for your use case.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hmmmm, I hate to argue, but this is not correct. If you are running a full factorial on 4 factors at 2 levels, the 15 DF's are assigned as follows:
4 DF: 4 main effects,
6 DF: 6 2nd order interaction effects,
4 DF: 4 3rd order interaction effects,
1DF: 4th order interaction effect.
There are no DF for estimating error. Just because you leave the higher order effects out of the model does not make them independent estimates of error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
@statman, I agree on the theoritical side, but on the practical side and by default, JMP does assume a model with only 2nd order effects when creating a full fractional design (so only main effects and 2-factors interactions).
I just checked also to be sure before posting ;)
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hmmm, Victor, not sure what you mean? JMP will create the full model. While the default order for JMP macros is 2, that does not mean JMP assumes a model with up to 2nd order effects. You just have to change the degree.
Again, while you may believe the higher order effects are negligible, you are pooling those effects to estimate the error. In fact, if you believe the higher order effects to be small, you are biasing the errors and therefore biasing the statistical tests. This error estimate is not the same as "pure error".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
@statman What I mean is that when you create this 4 factors full factorial design with the DoE platform "Classical", "Full Factorial", the default "Model" script created in the datatable creates a model up to the 2nd order only :
Again, i know this can be changed and that the full assumed model for a full factorial model is the saturated one you describe with 3 factors interactions and one 4-factors interaction, but I'm not sure new users or beginners may naturally change the default model in JMP and will refine the model only once launched by deleting some terms.
I did not use the term "pure error" in my initial response, in order to avoid any misunderstanding, but it seems my response was not clear enough.
Thanks for the discussion and the added informations that will certainly help @VarunK get a better understanding.
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Thank you Victor, for your detailed answer.
I will go through the links that you have provided.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Replication is a strategy to handle noise (factors that vary but are not explicitly manipulated during the experiment). There are multiple ways to do replication (e.g., RCBD, BIB, Randomized replicates), but in all instances you would need to replicate the exact same treatment combinations in your factorial design. Your proposal would not do this. Your design has 16 different treatment combinations and no replicates.
You do have options. Much depends on how significant you predict higher order effects to be active (e.g., I'm not sure why you need to estimate 3rd and 4th order effects?) If, for example, you are willing to compromise the ability to separate and assign 2nd order+ effects (e.g., alias these effects), you could run a fractional res IV design in 2 complete blocks. You could also do a res V in 2 incomplete block in 16 runs.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Query on generating DOE with four (2-level) variables and analyzign 2 variables at a time
Hello statman:
Thank you for your reply.
I had looked at the half factorial run earlier, but as you mentioned, this results in aliased interactions.
Based on the issue that I am facing, I believe that there might be an interaction of two factors which is resulting in the issue.
If that is the case, I want to identify them in the first trial and hence I was going for the full factorial.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us