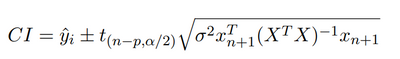- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Prediction and confident interval for DOE with random block?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Prediction and confident interval for DOE with random block?
I have a custom design in the attachment which has 5 continuous factors, one categorical factor with three levels, this design has 36 experiments in 6 blocks due to equipment limit. The results in this file are simulated instead of actual results. I used the default model, and then remove terms which PValue >0.05 one by one in the effect summary, and finally I got a model. However, in the prediction profiler there is a Random Block[1-6], I have to choose one of them, which doesn't make sense because the new experiment will be a different block. How can I choose different block instead of 1-6? I added a new row in the JMP file, which can predict new value, but without confident interval. How can I get the confident interval? I knew we can calculate CI based on the formula below. For the DoE with random effect, what's formula for confident interval calculation? Should I add the average value of random effect on top of CI?
Thank you so much for your help.
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hi @lazzybug,
You have the choice in the Profiler to choose between "Conditional Predictions" or non-conditional predictions (in the red triangle of the Profiler, check if the option "Conditional Predictions" is checked, just before the last option of the menu "Appearance").
As you mention, "Conditional Predictions" lets you choose the level of the random block (so you will end up with smaller confidence intervals, since the random block effect is no longer random but more like a fixed effect you can choose), whereas when the conditional option is unchecked, the random block effect is taken into account for the variance of predictions (you can't choose the level of the random block and you end up with larger confidence intervals).
- In the case of "Conditional Predictions", new future runs will be attributed to a new block, but since the effect of this new block is still unknown, it has an offset value of 0 by default (it is not possible to know in advance if new runs in this block will be on average higher or lower than previous runs from different block, so it has no offset).
- In your case, you can uncheck "Conditional Predictions" and Look at the prediction formula in the red triangle next to "Response Y", "Estimates", "Show Prediction Formula". You may have a similar formula as this one (and you can verify that random block levels are not present in this formula) :
You can save formulas for the response, and for lower/upper 95% CI. This will give you predictions taking into accound the random block effect, and may be more relevant in your case.2.41318058401651 + 1.08446092046299 * :X1 + 0.672993409088489 * :X2 + 1.00977007848638 * :X3 +1.41114309105797 * :X4 + Match( :X6, "L1", 1.46585081504277, "L2", -1.30266943360671, "L3", -0.163181381436053, . ) + :X1 * (:X2 * 1.58560226366689) + :X2 * (:X3 * 1.30368310940107) + :X3 * (:X3 * 3.86103114153648) + :X2 * (:X4 * 0.591689620884462) + :X1 * Match( :X6, "L1", 1.6824493957067, "L2", -0.835857163875241, "L3", -0.846592231831457, . ) + :X2 * Match( :X6, "L1", 2.20524178427256, "L2", -2.78718463269197, "L3", 0.58194284841941, . ) + :X4 * Match( :X6, "L1", 3.57200821808011, "L2", -3.45349090461962, "L3", -0.118517313460483, . )
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hello @lazzybug,
Looking at your file, here are some comments that may help you :
- Looking at your model, I have rebuild the model step-by-step (with same personality, emphasis and method) to see if I would find the same results as for the model you have saved. I have a slightly different model, less "parcimonious" as I have three more terms in my model : X1*X6, X2*X3 and X2*X4. When comparing the two models, I see that having three more terms in the model enables to have a higher R² (0,95 vs 0,86), higher R² adjusted (0,90 vs 0,79), a lower RMSE (1,51 vs 2,13) and a lower p-value for the model (<0,0001 vs 0,0003), even if my last term X2*X4 has a p-value above 0,05. This significance level helps you to sort out the significant from non-significant factors, but it shouldn't be your only guide in the modeling/analysis phase. You should also take a look at how well does your model explain the response (with metrics like R², R² adjusted, ...) and how accurate it is (with metrics like RMSE). It may be better to stop removing terms even if one is above the threshold 0,05 if you have found a more reliable model. You may also take a look at the residuals : it can also show curvatures or patterns that may help you determine there might be still a missing effect. Also if possible, evaluate the final model and compare it with domain expertise : does the model make sense ? Would you expect some effects/terms to be negligible or important ? See the script "Fit Model 2" in the JMP datatable for more details about the model I found.
- In your "Fit model" platform, since you have specified and introduce a random block, it might be interesting to know if this random block is a significant term is the model or not, or said otherwise in your case : is there a block effect on my results due to my equipment limit that I should take care/use in the modeling ? Looking at the panel "REML Variance Component Estimates", you can see that the Wald p-value is above the threshold of 0,05 meaning that the block effect is not significantly different from zero. That gives you an indication that this block effect may be removed in future experiments ore in the analysis. More infos here : Restricted Maximum Likelihood (REML) Method (jmp.com)
- In my case, when clicking on red triangle of "Response Y" and next "Factor Profiling" and "Profiler", the random block does not appear. You have it in your model's profiler (Conditional Profilers (jmp.com)), because the option "Conditional Predictions" is checked in the red triangle of your profiler. If you uncheck it, you'll no longer see this random block effect and the values of the 95% confidence interval will also change to reflect this change.
- Once this is done, you can save the "Prediction formula" and "Mean Confidence Interval" through the red triangle, "Save Columns" and choose the appropriate formula. You shouldn't see with the previous steps the random block in the formula.
Hope this will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hello @Victor_G, thank you so much for your quick response. Your explanation is very help. I still have one question, as you mentioned the random effect is not significant. I removed the block in the model, and remove the term which pvalue >0.05, and I got a totally different model(Fit model 3 in the JMP file), which R2 adj is pretty low. Could you please explain at what situation we have to include random effect in the model or not? Thank you so much again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hi @lazzybug,
I might have answered a little too quick on the random block effect and the suggestion to remove it, sorry for that.
A general question before my comments/answers : do you know the true model behind Y (since you were talking about simulated results) in order to compare the different models with the "true" simulation model ?
The random blocking effect helps you to reduce noise in the analysis by creating blocks where the variability within a block will be small. This process helps you determine and sort out more easily significant effects.
- On a "conceptual" level, since you have designed your DoE with it, it seems more relevant to keep this random block effect.
Even if non-significant, your random block effect seems to be quite effective at removing noise from the experiments, as it captures 70 (in your first model) to 83% (in the second model) of the total variance trough this block effect. So even if non-significant, you certainly gain more precision in your model by keeping it (this can be seen also comparing RMSEs of your models 1, 2 and 3).
- On an "analysis" level, keeping your random block effect helps you reduce variance in your model (and predictions).
What are the consequences of removing the random blocking effect ?
- The unexplained error in the model will be larger (as you can see looking at the RMSE of your model 3 compared to models 2 and 1),
- Therefore, the test of the treatment effect might be less powerful, so you might miss/remove some significant effects due to the increased "noise"/error (that's why you may end up with a more parcimonious model in model 3).
- The parameter estimates values and standard deviations may change (this is also seen when adding/removing an effect in the modeling).
In this present case, unless you have the true simulated model for Y to know which model performs best, it is hard to choose one model in favor of another, since they are very close from each other (looking at which effects are in the model and their parameter estimates). You can also compare the different prediction profilers (see script "Comparison of models - Profiler" in the datatable), they seem to be in accordance about importance of factors and what level for each factor seem to be the optimum. There are some differences on the curvatures of some factors (for example X1 has some curvature in model 3, whereas X3 has some curvature in model 1 and 2 with random block).
I would still prefer model 2, as it takes into account random blocking and seems to have better "performances", but this may not be the definitive choice.
At the end, let's remind from Georges Box that : "All models are wrong but some are useful". The choice of the model should also be done in consideration of its "usefulness" and in accordance with domain expertise.
If in doubt, you can still add some validation runs that may help you see/compare which model(s) generalize better than the other(s).
Sorry for this "non-deterministic" answer, but I hope this will help you,
Happy New Year !
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hi @Victor_G, I greatly appreciated your explanation, I have much better understanding about the random effect in the DoE data analysis. As you mentioned that we can keep the model better to fit the existing data with high R2 adj and less RMSE. I still have one question about random effect about prediction. I did notice that the prediction formula is conditional, which means it has different offsets for different blocks, but it's zero for the future run. Is it true? I tried to fit some model which random effect is significant, but the prediction offset still has a zero. Could you please explain my question? Thank you so much for your help again.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction and confident interval for DOE with random block?
Hi @lazzybug,
You have the choice in the Profiler to choose between "Conditional Predictions" or non-conditional predictions (in the red triangle of the Profiler, check if the option "Conditional Predictions" is checked, just before the last option of the menu "Appearance").
As you mention, "Conditional Predictions" lets you choose the level of the random block (so you will end up with smaller confidence intervals, since the random block effect is no longer random but more like a fixed effect you can choose), whereas when the conditional option is unchecked, the random block effect is taken into account for the variance of predictions (you can't choose the level of the random block and you end up with larger confidence intervals).
- In the case of "Conditional Predictions", new future runs will be attributed to a new block, but since the effect of this new block is still unknown, it has an offset value of 0 by default (it is not possible to know in advance if new runs in this block will be on average higher or lower than previous runs from different block, so it has no offset).
- In your case, you can uncheck "Conditional Predictions" and Look at the prediction formula in the red triangle next to "Response Y", "Estimates", "Show Prediction Formula". You may have a similar formula as this one (and you can verify that random block levels are not present in this formula) :
You can save formulas for the response, and for lower/upper 95% CI. This will give you predictions taking into accound the random block effect, and may be more relevant in your case.2.41318058401651 + 1.08446092046299 * :X1 + 0.672993409088489 * :X2 + 1.00977007848638 * :X3 +1.41114309105797 * :X4 + Match( :X6, "L1", 1.46585081504277, "L2", -1.30266943360671, "L3", -0.163181381436053, . ) + :X1 * (:X2 * 1.58560226366689) + :X2 * (:X3 * 1.30368310940107) + :X3 * (:X3 * 3.86103114153648) + :X2 * (:X4 * 0.591689620884462) + :X1 * Match( :X6, "L1", 1.6824493957067, "L2", -0.835857163875241, "L3", -0.846592231831457, . ) + :X2 * Match( :X6, "L1", 2.20524178427256, "L2", -2.78718463269197, "L3", 0.58194284841941, . ) + :X4 * Match( :X6, "L1", 3.57200821808011, "L2", -3.45349090461962, "L3", -0.118517313460483, . )
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us