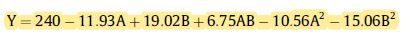- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Prediction Formula Equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Prediction Formula Equation
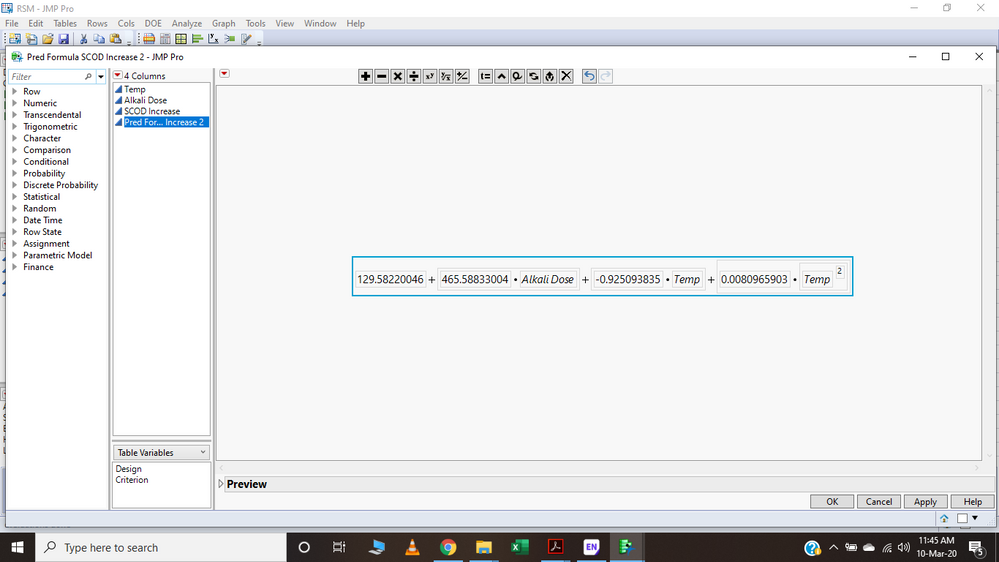
Dear and Respected All, Please help in sorting out this issue of getting the prediction final equation after applying RSM to a data. I have read several articles which have cited actual equation in different terms having constant and intercepts (image attached), the one JMP gives are having only numerical values (Image attached).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Hi @Afnanyasir,
Just to make sure, when you say you applied RSM to the data, do you mean a response surface model? Before applying that specific model, do you have a priori knowledge that this is the correct model to use, maybe from a physical or chemical equation that is known to model the specific kind of behavior? If not, what is the justification for choosing that particular model? If it's not based on a physics/chemistry model I recommend analyzing this with GenReg, which you can do since you have JMP Pro.
The model that you show doesn't look like a complete RSM because, as you show in the equation below, your model doesn't have the mixture term A*B and is missing one of the quadratic terms. Otherwise, your equation is perfectly fine. You have the intercept, the first number, the slope for dependence on Alkali Dose, slope for the dependence on Temp, and slope for the dependence on Temp^2. Did the other terms drop out because they were not contributing to the model?
You can always manually enter in the other terms to get the full RSM and re-run the model. Note of caution: be careful how many terms you include in your model so you don't over-fit. Your current model has three terms in it, so you need at least 4 rows in your data table to ensure that you have at least one degree of freedom. If you are trying to predict an outcome, you'll want to test it out on some data that was not used to fit the model, or at least do some verification runs to make sure your model is correct. If you have enough rows in your data table (maybe >100 or so), you might be able to do cross-validation and find a best-fit empirical model.
Hope this helps,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Hello @SDF1 Sir/Maam. Thank you so much for your detailed reply. Yes by RSM I mean response surface model and i had prior knowledge about the model which i was going to use according to my data. For cross check my supervisor ran the same data through another software which confirmed that the data behaved in a linear way (increasing way) and also the regression plot in JMP explained the data in a linear way. If i include all my terms or say independent variables and their mixture the equation becomes more complicated (image attached) and is listed as non-significant,so basically I didn't include them in running RSM as they were described as non-significant. Factor A, B are significant while A*B, A2 and B2 are termed as non-significant (image attached). so do I have to run the non-significant terms as well to get complete formula? and if I add all the terms then how will i express the final equation (image attached)?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Hi @Afnanyasir,
If you have prior knowledge about a model, then just use that functional form.
For example, in physics, if an object falls from height "h" with a certain initial velocity (v0), then the vertical position of the object (as a function of time) is (g is gravitational constant):
y(t) = h + v0*t + (1/2)gt^2
If the experiment you're doing involves falling objects, then you would use this equation and no other, so it's not an empirical formula, but a first-principles formula. If you have a first-principles formula from physics or chemistry, go ahead and use it.
But, based on what you're saying, it sounds like from previous work that you have an indication it's a linear model based on alkali dosage and temp, and just wanted to check if there were any cross terms or higher order terms to it. By running it through a RSM, you can get a good indication as to what factors might be important or not. However, that p-value you point to is more about the parameter estimate value and whether or not it falls within the 95% confidence interval. So, all it means is that the parameter estimate is not very good.
If you want to know whether a term, such as A*B or A^2 or B^2 should be in a model, I recommend running it through the stepwise or GenReg Personalities in the Fit Model platform. You could also try a PLS or GLM personality and see what you find there.
As an example, with the Big Class.jmp example data, you can run an RSM on age using height and weight as "A" and "B". If you do that, the Effect Summary plot tells you which factors (and combinations) are relevant, if their P-value is << alpha. These are the kind of p-values you want to look at.
For your work, it sounds like your response, SCOD Increase is just linearly dependent on Temp and Alkali Dose. Whatever is the simplest model and one that you can verify, then go for that, by all means.
As a last bit of advice, if you have a small data set, you might want to look at validating the model, you should look into the autovalidation JMP add-in and see if that can help you.
Hope this helps!,
DS
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
So do i need to add the non-significant parameter estimates in RSM to get final equation? or do i just need to skip them? because the final equation changes if i include or exclude the non-significant parameters. Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Sorry for my ignorance, but some of your information is conflicting. You say you want to analyze the data from your data set using RSM (built in JMP model construction I presume)...this includes main effects, 2nd order effects (2-factor interactions), and quadratic effects (e.g., A+B+AB+A^2+B^2). This model does not assign quadratic interaction effects (e.g., A^2B, AB^2, A^2B^2), as these are assumed to be estimates of error (I won't debate this here). In your last reply, you suggest the model is only linear? Also you mention"mixture". So is this a mixture design? RSM is not how you would typically analyze a mixture design (with the associated constraints).
There are a couple of thoughts:
1. Start with a saturated model (assign all degrees of freedom). Simplify the model by removing insignificant terms (use scientific theory, RSquare and RSquare Adj values and the delta between those, standard errors and normal plots to help select the significant factors). Re-run the simplified model to get residuals to assess model assumptions. If the quadratic terms are insignificant, take them out of the model.
2. If you are truly at a point where you are optimizing to develop the best prediction equation, significance is not the main concern. This should have already been determined and so now you are just filling the space of the optimum design region.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Thank you for a detailed reply. As I said earlier the data regression plot explains the data in a linear way also the quadratic models and other polynomial models are termed as non-significant in parameter estimates. only the individual A factor and Individual B factor are termed as significant. My question is do i need to include the non-significant terms such as AxB or A2B2 in my RSM model to get the final equation? or do i only add the significant ones which are individual A and B factor?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Prediction Formula Equation
Hi @Afnanyasir,
Before dropping the mixture term, A*B, and the quadratic terms, A^2 and B^2, I recommend using the Fit Model platform and testing out the RSM model, but use the GLM, GenReg, or Stepwise "Personalities" to see which terms in the polynomial expansion of the RSM are really insignificant in the model. Try some other methods to fit the data and see what they give. If they're all giving similar results that the A*B and quadratic terms are insignificant, then drop them in the final model. If the data was gathered via a RSM DOE, it doesn't have to be analyzed through that same platform. You can analyze it other ways as well.
Hope this helps,
DS
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us