- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Plan optimal // facteurs catégoriels
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Plan optimal // facteurs catégoriels
Bonjour,
Lorsque je passe pas la plateforme plan optimal :
- je fais un plan avec 3 facteurs catégoriels chacun avec 3 niveaux + j'ajoute seulement les 3 effets principaux => 18 essais recommandés
- je fais un plan avec 3 facteurs catégoriels, 2 facteurs avec 3 niveaux et 1 facteur avec 4 niveaux + j'ajoute seulement les 3 effets principaux => 12 essais recommandés.
Pourquoi il y a moins d'essais pour le 2nd plan alors qu'il y a plus de niveaux de facteur pour un des facteurs catégoriels ?
Merci d'avance
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Plan optimal // facteurs catégoriels
A little mistake in the post : When I use CUSTOM DESIGN plateform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Plan optimal // facteurs catégoriels
Hi @Charlotte1,
Welcome in the Community !
A part of the answer may be found here about how is computed the "Default" number of runs in the Custom Design platform : Design Generation (jmp.com) : "This value is based on heuristics for creating a balanced design with at least four runs more than the Minimum number of runs."
When reproducing your examples, here is the situation :
- In your case 1, the minimum number of runs is 7 : you have 1 intercept, and 2 terms for each 3-levels categorical factor (number of levels-1, since the last level estimate can be calculated from the others : L1+L2+L3 = 0). JMP could recommend 11 runs (7 minimum runs for main effects estimation + 4 extra runs), but this number leads to the creation of an unbalanced design, where not all factors are estimated as precisely and uniformly as they could. So JMP is calculating the minimum number of runs to satisfy the condition to have a balanced design with at least four more runs than the minimum number of runs (and in this case with only uneven number of levels for your factors, it leads to 18 runs).
- In your case 2, the minimum number of runs is 8 : you have 1 intercept, 2 terms for each 3-levels categorical factor and 3 terms for the 4-levels categorical factor. When adding 4 more runs, you can obtain a balanced design with 12 runs, so this is the suggestion JMP does.
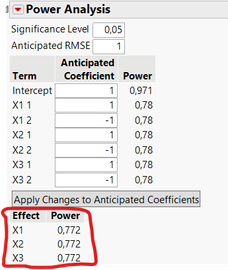
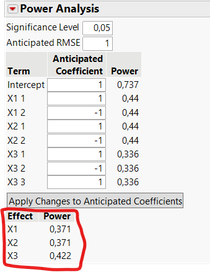
Be careful however, this default setting may not be the optimal one in your use cases and there are other characteristics to evaluate. For example, looking at the power analysis (capacity to detect a statistically significant effet if there is one), you can see that the two designs are clearly not equivalent :
Use case 1 with 18 runs vs use case 2 with 12 runs :
And the same comparison and analysis could be done for prediction variance (higher prediction variance with 12 runs than with 18 runs), and looking at the differences for the aliases in the designs, etc...
You can also compare quickly the number of runs by default for estimating main effects compared to the number of runs if you did all combinations between factors lelvels :
- In the use case 1, you have 3^3 = 27 possible combinations.
- In the use case 2, you have 4x3x3 = 36 possible combinations.
So quite intuitively, even if both designs may use the "default" number of runs, they don't cover the same experimental space of all combinations : in the use case 1, you cover 66,7% of all possible combinations, whereas in use case 2, you cover only 33,3% of all possible combinations, hence the higher power for factors, lower prediction variance, ... in use case 1 compared to use case 2.
I hope this answer will help you,
"It is not unusual for a well-designed experiment to analyze itself" (Box, Hunter and Hunter)
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us