Plackett-Burman Folded

[#1]

Hello,

When is Plackett-Burman Folded DOE useful when compared to classical Plackett-Burman DOE of resolution IV Fractional Factorial Design?

Kind regards,

Sara

[#2 · Accepted solution]

P-B designs have some advantages over regular FF designs, including the design size increasing four runs at a time instead of doubling. On the other hand, they have correlated effects, which puts off some experimenters. I see this as an advantage. I can estimate correlated parameters, albeit with inflated variance. I cannot estimate confounded effects via an FF design. I eliminate model bias if I estimate correlated terms. I suffer model bias if I exclude confounded terms. The fold-over runs will reduce the correlations when using the P-B design, as they reduce the confounding with FF designs.

[#3 · Accepted solution]

Hi @SaraA,

I'm not sure I fully understand your question, but I will provide a first discussion starter.

• Plackett-Burman are usually Resolution III screening design, meaning that main effects are correlated with 2-factors interactions. Only main effects are estimable with some precision (without correlations between each others and with the assumption that interactions and higher order terms are negligible).
• Resolution is a measure of the degree of confounding in an experimental design (Resolution in Screening Designs):
  • Resolution III means that some main effects are confounded with one or more two-factor interactions. In order for the main effects to be meaningful, these interactions must be assumed to be negligible.
  • Resolution IV means that main effects are not confounded with other main effects or two-factor interactions. However, some two-factor interactions are confounded with other two-factor interactions.
  • Resolution V means that there is no confounding between main effects, between main effects and two-factor interactions, and between pairs of two-factor interactions. Some two-factor interactions are confounded with three-factor interactions.
  • Resolution V+ means that the design has resolution greater than 5 but is not a full factorial design.
  • Resolution VI means that there is no confounding between effects of any order. The design is a full factorial design.
• Plackett-Burman designs are efficient screening design for main effects, but may need augmentation to augment main effects estimates precision and to investigate 2-factors interactions (and other higher order terms). In order to do this, you can :
  • Augment your design and specify a model, so that the platform will optimally augment your initial PB screening design with new runs to be able to estimate the new terms added in the model : Example Using the Augment Design Platform
  • Augment your design by doing a foldover. This create the same additional number of runs of the original design with the same values for the factors, except for the factor over which the foldover is done, the new runs will have values mirroring the initial set (-1 instead of 1, 1 instead of -1, rest of the factors values stay the same). This is helpful to remove the confounding of two-factor interactions and main effects : Create a Foldover Design

As different designs may be helpful depending on the situation, I can only suggest to try creating several designs and compare them before choosing one and doing the experiments.
As a general remark, the higher the resolution, the higher the number of runs required, so you need to evaluate the tradeoff between what you want to discover/evaluate and your experimental budget constraint. Also depending on the construction and type of classical design (fractional factorial, Plackett-Burman or others) you may not have a lot of flexibility on the run size step/increment (as an example, here is the possible designs list for 5 factors from the 2-levels screening design platform) :

You may find a higher flexibility in run size, model specification, and better handling of constraints by using the Custom Design platform.

Hope this first discussion starter may help you,

[#4]

Hi Victor_G and Mark_Bailey,

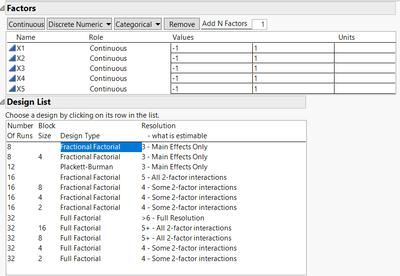
Thank you for these explanations. The reason I was asking about the Plackett-Burman Folded is because I get this as one of the options when attempting to design a screening DOE:

Therefore, I was curious about the added value of the P-B Folded when compared to P-B and FF design.

Moreover, when designing the experiment, I get the options to add center points. I understand that adding center points helps in the estimating the lack of fit as well as curvature in the response but I am unsure about how many center points should be added? Is there any value of adding more center points with regard to estimating the curvature?

[#5]

Hi @SaraA,

Ok I understand better your question and the design mentioned.

The 24-runs option "Plackett-Burman Folded" you see corresponds to a foldover of the first design PB (resolution III) shown in your screenshot (with 12 runs).

You can reproduce the 24-runs Plackett-Burman Folded design highlighted by using the 12-runs Plackett-Burman design, and then augment the design using a foldover (without specifying a factor for the foldover). You'll then see that the new 12 runs added to the original PB design are just mirror experiments (levels are inversed between original experiments and new ones, -1 instead of 1, and 1 instead of -1), in order to uncover aliasing and enable identification and estimation of some 2-factors interactions.

About centre points, 3 to 5 is usually a good range, as it enables to detect quite precisely curvature, without biasing the lack-of-fit test with too much centre points experiments. Please remember that adding centre points may help in detecting curvature, but you won't be able to link this curvature to specific quadratic effects of your factors. You will only be able with centre points to fit one quadratic effect among all that may possible.

Some discussions that may interest you about centre points :

effect of centre points 

How many center points to add in a design? 

And JMP Help about centre points : Center Points, Replicate Runs, and Testing

Hope this answer will help you,