- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Obtaining 95% CI from predicted P (logistic)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Obtaining 95% CI from predicted P (logistic)
Hello,
I'm doing logistic regression in JMP 16. I would like to obtain the 95% CI around predicted P for some independent variables using the P as a measure of strength of association. I know the math to calculate the 95% CI from linear predictors but I need help pulling out the necessary information once I run the model. I can obtain the linear predictor by saving to a new column, but I also need the standard error of the linear predictor. How do I obtain that? I have done this in R but I would prefer to learn in JMP.
Thanks!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
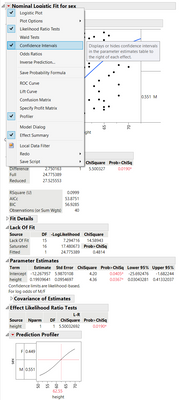
do the logistics modeling use Fit model you can turn on CI in the hotspot menu:
This will give you CI on the parameter estimates table.
From the same hotspot you can also save the probability formula's.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
do the logistics modeling use Fit model you can turn on CI in the hotspot menu:
This will give you CI on the parameter estimates table.
From the same hotspot you can also save the probability formula's.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
Thanks for reply. Turning on CI gives me the CI around the chiSq tests for each term, but what I'm after is obtaining a CI around the expected value (probability of "1" or "yes"). To calculate the CI, one needs the linear predictor as well as the SE. I can get the linear predictor and the expected value from the save drop down choices but I can't find where to obtain the SE of the linear predictor.
95% confidence interval formula:
Lp-1.96* se(Lp), Lp+1.96*se(Lp)
Lp - linear predictor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
...and to finish the thought, this is the formula to get CI around probabilities (expected values) once you have the linear predictor interval:
Lp interval [a, b]
Probability interval:
[exp(a)/1+exp(a), exp(b)/1+exp(b)]
[lower, upper]
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
Did you notice the Std Error column in the parameter estimates table?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
Thanks much! My bad. I thought it was for something else.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Obtaining 95% CI from predicted P (logistic)
Cool! If you are satisfied, please mark the topic as solved so that other people know it is done :)
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us