- JMP User Community
- :
- Discussions
- :
- Normal Distributions and Transformations
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Printer Friendly Page
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Normal Distributions and Transformations
Hi Everyone,
I have some measured data and when I try a continuous normal fit, I can see that my data is not normal. However, I can see from the Goodness-of-Fit Test that the data is from the Johnson Su distribution.
This distribution has two shape, one location and one scale parameter. From my research online, I can see how to calculate variance from these parameters and from that the standard deviation. I used Excel to calculate that, but is there a way in JMP to do this? From my understanding, the Summary Statics table from the "Distributions" analysis calculates these statistics assuming the data is from the normal distribution.
Thanks in advance!
Natalie
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Hi Jim,
I have the same issue. I have modelled some Johnson Si transformed data, and got a predicted model. I tried to use the inverse function to transform the predicted data back, but it's not working. Would you be able to provide more guidance on writing a script to do this? I keep coming across these types of distributions when modeling responses from DOE experiments, so it would be really useful to know how to transfer the data back.
Many thanks!
Christel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Here is a function that I pulled out of a running system that uses Successive Approximations to get the resolved values
/***********************************************************************/
/* */
/* The getformula column retrieves the formula from the translation */
/* column and replaces the Original Column name in the formula with */
/* string "__value__". The value of this variable is what will be */
/* evaluated in the successive approximations done by the script. */
/* */
/***********************************************************************/
getformula = Function( {ColName, FormulaColName},
{ColName, FormulaColName, TheFormula, coloncolname},
//__value__ = .;
// Get the transformed data columns formula as a literal string
TheFormula=Column( FormulaColName ) << Get Formula ;
// Check to see that a formula was found
If( Is Empty( TheFormula ) == 1 ,
Dialog(
" The column specified as",
"the Transformed Column does",
" not contain a formula. ",
" ",
" Please rerun and select",
" the correct column"
);
Throw();
);
TheFormula=char( Column( FormulaColName ) << Get Formula );
// Get the actual name of the orignal column since
// the upper,lower case and spacing is critical in determining
// where in the formula the column name actually occurs
ColName = Column( ColName ) << Get Name;
// Determine if the reference to the column name in the
// formula is a simple :colname reference or a complex
// reference :Name(\!"colname\!")
// If the column name isn't found set the return code to -1
If(
Contains( TheFormula, ":" || ColName ), ColonColName = ":" || ColName, // Else
Contains( TheFormula, ":Name(\!"" || ColName || "\!")" ), ColonColName = ":Name(\!"" || ColName || "\!")", // Else
rc = -1
);
// Replace all of the column references in the formula with
// the string "(__value__)" so that when the formula is
// evaluated later, it will take the then value of the memory
// variable called __value__ and use it in the formula
If( Contains( TheFormula, ColonColName ) > 0,
While( Contains( TheFormula, ColonColName ) > 0, TheFormula = Munger( TheFormula, 1, ColonColName, "(__Value__)" ) ),
Dialog(
" The column specified as",
"the Transformed Column does",
" not contain a reference",
" to the original column.",
" in it's formula.",
" ",
" Please rerun and select",
" the correct column"
);
Throw();
);
TheFormula;
);.
/***********************************************************************/
/* */
/* The gettrans function evaluates the formula in the transformed */
/* and converts the formula into a generic form for repeated use in */
/* running of the script. */
/* */
/***********************************************************************/
gettrans = Function( {ColName, FormulaColName, TheTarget, Theformula},
{ColName, FormulaColName, TheFormula, High, Low, TheTarget, TheMax, Themin, __value__},
// The program uses successive approximations to determine the different
// parametrics. The way it works is that it calculates the needed parameter
// such as Mean, or Standard Deviation, and then by using successive
// approximations from the original column's values, and passing those
// values through the columns formula, when the approximation value matches
// the calculated value from the transformed column, the retransformed value
// has been found
// Set the extreem values
High = Col Maximum( If( Excluded( Row State( Empty() ) ) == 0, Column( ColName ), . ) );
Low = Col Minimum( If( Excluded( Row State( Empty() ) ) == 0, Column( ColName ), . ) );
Highm = 999999999999999999999999;
Lowm = -999999999999999999999999;
If( Highm > High,
High = Highm
);
If( Lowm < Low, low = lowm );
// Make a guess at the first value
__value__ = Mean( High, Low );
// Iterate the guessing for up to 100 times, adjusting by 1/2 on each loop
For( i = 1, i <= 100, i++,
TheResult = Eval( Parse( theformula ) );
If(
TheResult > TheTarget, High = __value__,
TheResult < TheTarget, Low = __value__,
Break()
);
If( High == Low, Break() );
__value__ = Mean( High, Low );
);
__value__; // Expose the return value
); // End of function gettrans
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Thanks for sharing this.
I'm only a scripting beginner, so it's a bit too complicated at the moment and I wasn't sure how to use it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Here is a complete program that returns a value based upon a statistic result from a transformed set of data. I hope this help
Names Default to Here(1);
dt=New Table( "Test",
Add Rows( 100 ),
New Column("PNP3",
Numeric,
"Continuous",
Format( "Best", 10 ),
Set Values(
[130.378809500886, 132.736937590235, 136.831952164704, 136.969154239163,
136.622623419893, 137.480356512481, 138.094011176166, 142.10586919757,
134.750041237898, 129.719685093372, 136.520172900026, 134.778624216716,
136.991131754497, 140.420940666186, 143.257827228986, 132.213765487819,
144.671172276421, 134.703176752174, 136.744212473486, 137.187637284245,
139.788226018039, 139.372617199359, 136.112484488985, 142.809097034809,
137.799370430979, 138.482493403385, 135.236982575217, 136.251777781494,
130.768356509183, 138.248554728086, 139.77894292052, 134.25405167366,
147.680687116943, 131.351711991517, 132.84274608728, 129.925216236015,
133.47206414316, 143.339607103893, 145.341236691691, 139.200187547183,
142.775409342827, 140.276696563388, 130.623979847275, 140.899814366103,
136.839389290019, 137.239125319, 133.5265281641, 139.356927352471,
130.278640163464, 144.604061001983, 135.286715550332, 134.465744849174,
131.37612790407, 131.830655714309, 140.69724979219, 142.88152043774,
135.253839945611, 127.349434776131, 129.499730399113, 128.447533754611,
130.916853702805, 134.599575929218, 140.761701916093, 136.870661473033,
138.253066182015, 140.403627077024, 134.522643679098, 124.842978178703,
131.803059455053, 125.886786494664, 133.013566701611, 136.940299158936,
133.263913979648, 144.695171321015, 149.541020434399, 144.503845528521,
136.086324063453, 139.530943158798, 138.421460162451, 133.180943784947,
142.166796633818, 142.676541730822, 135.723943440339, 143.957996114985,
145.712158558794, 138.38937502716, 140.535304753392, 142.140619481175,
131.379414509756, 144.949299702964, 133.349854687882, 139.470639804255,
140.160558367008, 137.130662662612, 145.692632562344, 131.870848869966,
136.391733804566, 134.219740661271, 139.021827550389, 147.958038547157]
)
),
New Column( "Johnson Sl Transform PNP3",
Numeric,
"Continuous",
Format( "Best", 12 ),
Set Property( "Notes", "Fitted Johnson Sl" ),
Formula(
(Log( (:PNP3 - 44.6529505888426) / 1 ) * 15.3554291860315 + (
-69.5611150866502)) * 1
)
)
);
/***********************************************************************/
/* */
/* The getformula column retrieves the formula from the translation */
/* column and replaces the Original Column name in the formula with */
/* string "__value__". The value of this variable is what will be */
/* evaluated in the successive approximations done by the script. */
/* */
/***********************************************************************/
getformula = Function( {ColName, FormulaColName},
{ColName, FormulaColName, TheFormula, coloncolname},
//__value__ = .;
// Get the transformed data columns formula as a literal string
TheFormula=Column( FormulaColName ) << Get Formula ;
// Check to see that a formula was found
If( Is Empty( TheFormula ) == 1 ,
Dialog(
" The column specified as",
"the Transformed Column does",
" not contain a formula. ",
" ",
" Please rerun and select",
" the correct column"
);
Throw();
);
TheFormula=char( Column( FormulaColName ) << Get Formula );
// Get the actual name of the orignal column since
// the upper,lower case and spacing is critical in determining
// where in the formula the column name actually occurs
ColName = Column( ColName ) << Get Name;
// Determine if the reference to the column name in the
// formula is a simple :colname reference or a complex
// reference :Name(\!"colname\!")
// If the column name isn't found set the return code to -1
If(
Contains( TheFormula, ":" || ColName ), ColonColName = ":" || ColName, // Else
Contains( TheFormula, ":Name(\!"" || ColName || "\!")" ), ColonColName = ":Name(\!"" || ColName || "\!")", // Else
rc = -1
);
// Replace all of the column references in the formula with
// the string "(__value__)" so that when the formula is
// evaluated later, it will take the then value of the memory
// variable called __value__ and use it in the formula
If( Contains( TheFormula, ColonColName ) > 0,
While( Contains( TheFormula, ColonColName ) > 0, TheFormula = Munger( TheFormula, 1, ColonColName, "(__Value__)" ) ),
Dialog(
" The column specified as",
"the Transformed Column does",
" not contain a reference",
" to the original column.",
" in it's formula.",
" ",
" Please rerun and select",
" the correct column"
);
Throw();
);
TheFormula;
);
/***********************************************************************/
/* */
/* The gettrans function evaluates the formula in the transformed */
/* and converts the formula into a generic form for repeated use in */
/* running of the script. */
/* */
/***********************************************************************/
gettrans = Function( {ColName, FormulaColName, TheTarget, Theformula},
//colname="PNP3";formulacolname="Johnson Sl Transform PNP3"; Thetarget=johnsonmean;theformula=myformula;
{ColName, FormulaColName, TheFormula, High, Low, TheTarget, TheMax, Themin, __value__},
// The program uses successive approximations to determine the different
// parametrics. The way it works is that it calculates the needed parameter
// such as Mean, or Standard Deviation, and then by using successive
// approximations from the original column's values, and passing those
// values through the columns formula, when the approximation value matches
// the calculated value from the transformed column, the retransformed value
// has been found
// Set the extreem values
High = Col Maximum( If( Excluded( Row State( Empty() ) ) == 0, Column( ColName ), . ) );
Low = Col Minimum( If( Excluded( Row State( Empty() ) ) == 0, Column( ColName ), . ) );
// Make a guess at the first value
__value__ = Mean( High, Low );
// Iterate the guessing for up to 100 times, adjusting by 1/2 on each loop
For( i = 1, i <= 100, i++,
TheResult = Eval( Parse( theformula ) );
If(
TheResult > TheTarget, High = __value__,
TheResult < TheTarget, Low = __value__,
Break()
);
If( High == Low, Break() );
__value__ = Mean( High, Low );
);
__value__; // Expose the return value
); // End of function gettrans
myFormula = getformula( "PNP3","Johnson Sl Transform PNP3" );
JohnsonMean = Col Mean(dt:Johnson Sl Transform PNP3);
show(JohnsonMean,colMean(:PNP3),Gettrans("PNP3","Johnson Sl Transform PNP3",JohnsonMean,myFormula));
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Hi Jim (@txnelson),
I couldn't understand how to transform a non-normal data to a normal distribution in JMP. Please may you explain the steps from a raw non-normal data to me?
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
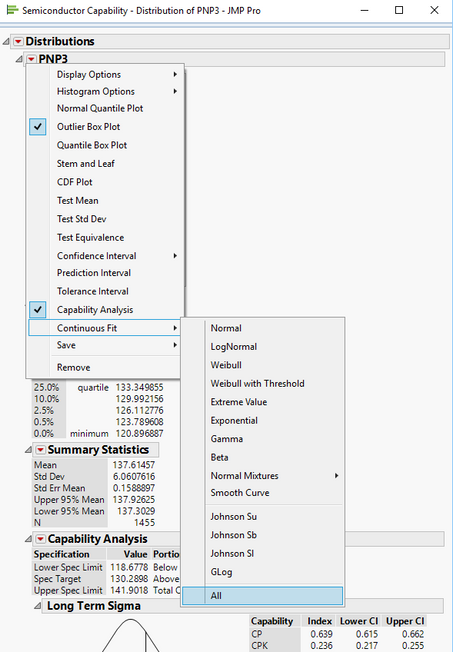
The Distribution Platform allows one to evaluate what Distribution a given column is, and then, it may have a method to transform the data to a normal distribution. Here are the steps
1. Run the Distribution Platform, selecting the desired column(s). My example comes from the Semiconductor Capability sample data table installed when JMP is installed.
Analyze==>Distribution
2. Once the output is displayed, select from the
Continuous Fit==>All
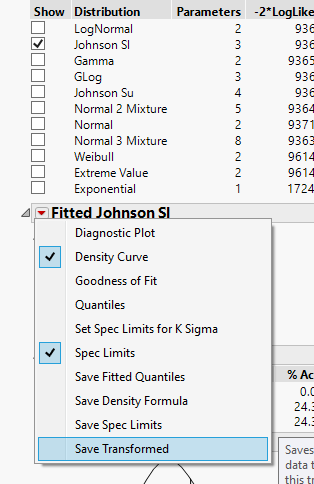
3. The platform will give you, in order, what distributions best fit the data. In this case, the LogNormal is selected. Unfortunatly, the LogNormal does not have the ability to create a transformed version of the data, so unselect it, and select Johnson SI.
4. Now, click on the red triangle for "Fitted Johnson SI and select Save Transformed
JMP has now saved a transformed version of the data into a new column, which you can now use for your analyses
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Hi Jim ( @txnelson ), thank you very much for your explanation!
I have the following problem:
1. For my study case, the non-normal outcome called OUT contains different timepoints (T1, T2, ...) because I have a repetead-measure design. So, when I do Analysis==>Distribution, I suppose I need to select that variable OUT as "Y, Columns" and the between-subject (e.g., Timepoints) as "By" in the "Cast Selected Columns into Roles" dialog, don't I?
2. If I do it then I will have a plot OUT vs. each timepoints such as OUT vs. T1; OUT vs. T2 and so on. In JMP v.10, I need to follow your instruction for each plot because it cannot do it automatically. It's okay. I select on Distributions Timepoint=T1==>Stack, and all plots are shown in the horizontal axis.
Doubt: Should I first select "Capability Analysis" or "Continuous Fit==>All"? I mean when I select "Capability Analysis" the dialog appears to enter the following parameters: "Lower Spec Limit", "Target" and "Upper Spec Limit", and I don't know which values I have to define. Are they based on the Box plot, excluding the outliers?
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
In addition, I am a beginner in JMP and this is my first transformation I try to do with an additional complexity that it refers to a repeated-measures design.
I couldn't find out the relationship between "Capability Analysis" and "Fitted Johnson SI" yet. I mean If I select the "Capability Analysis" first and assuming I enter those aforementioned parameters (my previous post) correctly, then I will select the "Continuous Fit==>All", choosing Johnson SI. In this way, does JMP take into account that information entered in "Capability Analysis" to evaluate the "Fitted Johnson SI"?
PS: My data is in tall (or long) format: rows are represented by subjects; the first column is Timepoints (T1, T2, ...) and the second column is OUT. When I clicked on Fitted Johnson SI==>Save Transformed for each timepoint, the same column called "Johnson SI Transform OUT by Timepoints" was completed with those transformed scores. After that I tried to run the stats analysis in Fit Model using that "Johnson SI Transform OUT by Timepoints" column in the "Pick Role Variables" box and {Timepoints, subject& Random, subject*Timepoints & Random} in the "Contruct Model Effects" box, but I couldn't get any relevant result.
I suppose I would need to run your script immediatly after getting the "Johnson SI Transform OUT by Timepoints" (transformed data) column. Am I right?
That's my next doubt: understanding your procedure described as solution. I ran your example and it was amazing! I need to learn how to "take the std from the transformed data, calculate what the values above and below the mean are for 1, 2, 3, etc. stds, and then reverse the transformation back to the original data.".
Thank you very much for your attention and valuable help!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
1. I suggest that you go to the JMP Webpage and read the documentation on the Distribution Platform
JMP Webpage==Support==>Online Documentation==Basic Analysis==>Distributions
It will give you a very good education on what the tool can do for you. You stated that you are using JMP 10. The most recent JMP version is 14(to be released shortly) and the documentation on the web is JMP 14. However, you will find, almost all of what you will read about in the documentation was available in JMP 10.
2. The determination of what the shape of your data's distribution (i.e. Normal, Johnson SI, Log Normal, etc.) is not determined by the Capability Analysis. It is actually the opposite. The shape of the distribution determines what formulas to use to calcuate the Capability of the data.
3. You seem to not understand what the limits are in a capability analysis. Spec Limits are traditionally determined from the knowledge of the measurement data. That is, if you are measuring voltage of an electrical component, the design of the part would state that for the part to work properly, the voltage needs to be between the Lower Specification Limit (LSL) and the Upper Specification Limit(USL). It would be these limits that would be used in the determination of how Capable the process is.
4. In many cases all you want to get out of the Distribution Platform, is to get the determination if the data are normally distributed. Why this is important, is because many statistical analyses have the assumption that the data are normally distributed. So the purpose of transforming the data is to change the data into a normal distribution, so the statistical tests can provide more accurate results.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Normal Distributions and Transformations
Hi Jim (@txnelson),
Thank you for your post. I read that link you had suggested. As I understood, I could fit the distribution using Johnson SI through Capability Analysis, selecting "Johnson SI" on the <distribution type> or I could run the Fit Distribution and then clicking on the red triangle Capability Analysis I could find the Spec Limits as you suggested.
I agree with you that Spec Limits are traditionally determined from the knowing of the measurement data. However, I believe that it applies to the engineering field. In Psychology field, it's hard to have any idea about those limits, but only the data collected. In this way, I think I should run the Fit Distribution for Johnson SI and then click on the red triangle ==> Set Spec Limits for K Sigma, selecting K value = 3.
When I do it, I get the Quantile Sigma and the fitting plot for Johnson SI. However, I haven't got the normal shape of my data, but only the parameters (Spec Limits) from Capability Analysis. What's the next step, please?
Thank you.
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us