Hi,
I Designed a set of experiments using Latin Hypercube Design (3 Factors), ran all the simulations (CFD simulations), and now I am analyzing the responses using Gaussian Process.
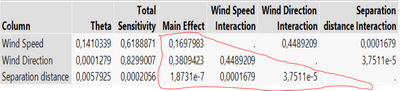
What does mean each term in the table named Model Report?
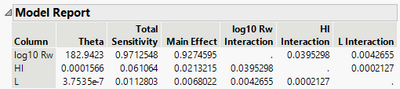
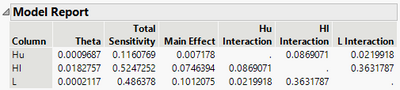
I believe that larger numbers (for example in the main effect column) mean that the factor has a more important effect on the response. Is that right? For example, in this figure, the more important factor would be the wind direction, and the effect of separation distance does not affect significantly the response. Is this interpretation alright?
How should I interpret the theta and total sensitivity columns?
I would like the analysis method not only to give me the correlation equation (model), but also a kind of screening, pointing to the most relevant factors in the problem. Is there any other analysis that may be better for this than Gaussian Process?
How should I analyze if the model fits well the results when using the Gaussian process, is there a criterion or rule of thumb that I should follow?
I'm new using JMP and Gaussian Process, so forgive me if my questions are too basic.
I don't know fluid dynamics. Please don't hesitate to comment if my response does not make sense to you.
What you said about importance is mostly correct, but maybe incomplete. I circled out all the numbers that you should look at. They include all entries in Main Effect, and off-diagonal elements among interactions. Wind Direction is the most important single effect, but the interaction between Wind Speed and Wind Direction seems to have slightly bigger effect. In this case, even Wind Speed has comparably much smaller contribution, one should not rule it out from the model. In general, the numbers that I circled out should add up to one. All main effects and interactions contribute to the total prediction uncertainty.
It might be safe to say Separation Distance is not important in this example. And you might be able to see how it will affect prediction by removing it.
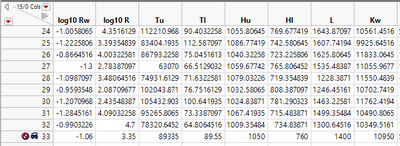
I use "Borehole Latin Hypercube.jmp" sample data as an example to explain. Please following this page to find the data: Example of a Gaussian Process Model
First I add a new row to the data table. The values are the means of individual columns, from the first column all the way through column "Kw". I hide and exclude this row, so it won't enter my analysis. I will use this row later to make my point.
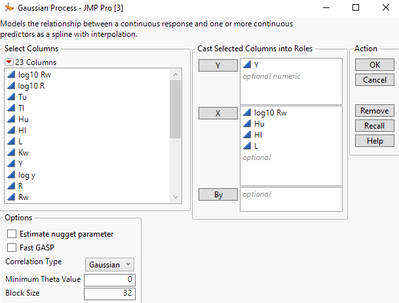
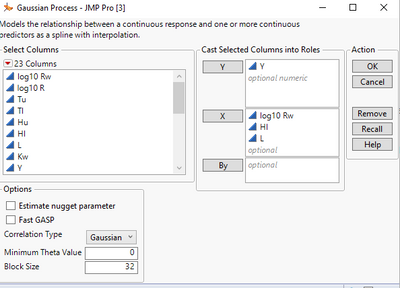
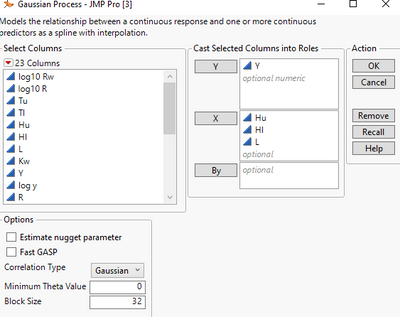
I fit a different model from the one on that example page. The model that I am going to fit will be more appropriate for this discussion. Here is how I configure the launch dialog:
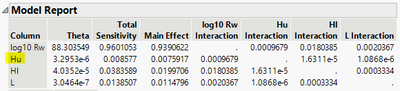
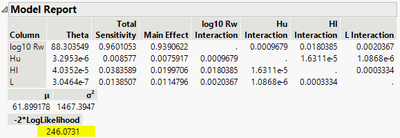
Here is the report, and seems Hu is relatively unimportant.
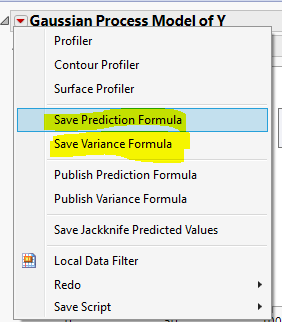
Before I rule out Hu, I save Prediction formula and Variance formula using the following two menu items.
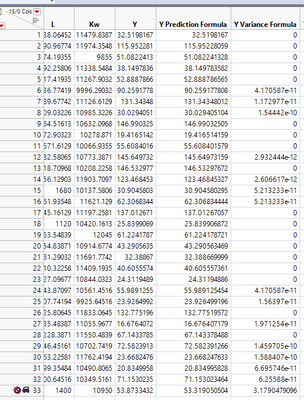
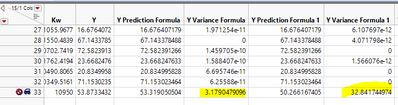
And you should see two more columns in the data table. Notice all Y predictions (except the one for the row that I added) equal the corresponding Y, and all Y variances (except my added row) are zeros. This is what we should expect from Gaussian Process models. (The platform has an additional feature, for which case, the statement no longer holds. But that is beyond what we are discussing here.)
Notice, for the added row, the prediction and variance are for the new X values. The X values that I picked are just sample means. You may enter the values that you are interested in for prediction, and you may enter multiple rows if you are interested in predictions at multiple sets of X values. Just don't forget to hide and exclude your added rows, so they won't affect inference.
Now I remove Hu and fit a new model. Here is the dialog configuration.
And here is the report
And I also save prediction and variance columns from this model. And here is the screenshot around the last row. And we can see variance is "much" larger.
Just to have a sense how wrong it can go, if I remove an important effect. I fit the third model, by removing "log 10 w" (the most important one) from the first model. Here is the dialog configuration.
Here is the report.
Also I save Prediction and Variance formulas from this model, and here is the screenshot around the last row. And notice how much variance increases.
So, for your data, before you decide whether you want to remove the last factor, you may want to check out how it will affect your predictions if you remove it.
For Theta, I cannot think of anything specific about their interpretation. They are model parameters; see Models with Continuous Predictors It is those numbers that I circled out, which are calculated based upon the parameters, are more interesting and interpretable.
"Total Sensitivity" are the sum of entries under Main Effect and Interaction Effects on the corresponding row. One may interpret them from a "marginal" perspective, maybe? I am not sure about this. But I guess that it might be useful if one does not want to go into too deep into interactions, but meanwhile it is insufficient to just bring up the entries under Main Effect.
All above should answer the question on how to screen and point out important factors. I am not sure whether there are "better" models than Gaussian Process model. But to my understanding, the success of its major applications in computer experiments, e.g. the ones related to CFD, is because it can approximate more complex mathematical models (I guess they mean PDEs.) And I am not aware of other models have such advantage.
About assessing the quality of Gaussian Process model fit, the -2Likelihood value might be useful. But I don't know enough about model selection in the Gaussian Process modeling context, I am not able to comment more on this.
