- We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- JMP 19 is here! Learn more about the new features.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Missing confidence intervals from orthogonal regression
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Missing confidence intervals from orthogonal regression
Hi,
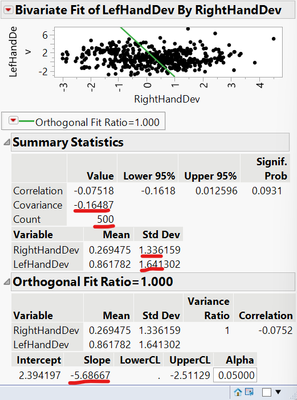
I'm using an orthogonal regression analysis on some data I have modelling the covariance of deviations made the left (y-axis) and right (x-axis) hands during a bilateral reaching task. For the most part, I am able to use the confidence intervals for the slope that JMP provides but on some analysis either the lower, upper or both confidence intervals are not calculated (a period is provided instead of a numerical value) and I can't seem to work out why.
I checked the JMP documentation (here: https://www.jmp.com/support/help/en/17.0/index.shtml#page/jmp/statistical-details-for-the-fit-orthog...) which directs me to paper (https://www.jstor.org/stable/1270564) that was used to calculate the confidence intervals, but I'm struggling to find anything from it that would explain why in some situations the CIs cannot be found, partly due to my limited mathematics ability/knowledge. Its not necessarily a problem that they can't be calculated but I would like to be able to describe why in some cases its not possible.
I'm using JMP Pro 16 on a macbook with the Ventura 13.0 OS and have provided a screenshot of the output. The data includes ~500 points per fit but is poorly correlated in some conditions. However, in other cases I have tried this doesn't seem to be a limiting factor. An example dataset is attached that I used to create the example outputs in the screenshot too if thats helpful,
Thanks,
Nick
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
Hi @OrderedMongoose ,
As you described in your question, JMP calculates a confidence interval as described in the Tan and Iglewicz 1999 reference.
You can use the following script to compute a confidence interval using a parameter that JMP generates (covariance and so on).
n = 500;
gamma = 1; //Ratio
t_dist = t Quantile( 1 - 0.025, n - 2 );
s_yy = 1.641302 ^ 2; //Variance of Y
s_xx = 1.336159 ^ 2; //Variance of X
s_xy = -0.16487; //Covariance of X and Y
phi = 1 / 2 * ArcSine(
t_dist * (2 / Sqrt( n - 2 )) * Sqrt(
gamma * (s_yy * s_xx - s_xy ^ 2) / ((s_yy - gamma * s_xx) ^ 2 + 4 * gamma * s_xy ^ 2)
)
);
beta_hat = -5.68667; //Estimate of Slope
theta_hat = ArcTan( beta_hat / Sqrt( gamma ) );
lower_confidence = Sqrt( gamma ) * Tan( theta_hat - phi );
upper_confidence = Sqrt( gamma ) * Tan( theta_hat + phi );
Show( Eval List( {lower_confidence, upper_confidence} ) );
Show( theta_hat - phi );
When calculating a confidence interval, beta(slope) is calculated from theta (beta equals tan(theta)). Theta is described in the reference. When calculating a confidence interval with your example data, the value of theta is less than -pi/2. In this case, a lower confidence interval (32.44) is greater than an upper confidence interval (-2.51), which is not reasonable. I think this is why JMP doesn't display a result.
Another approach is to use boostraping. Please see https://www.jmp.com/support/help/en/16.2/#page/jmp/example-of-bootstrapping.shtml#.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
Hi @OrderedMongoose ,
As you described in your question, JMP calculates a confidence interval as described in the Tan and Iglewicz 1999 reference.
You can use the following script to compute a confidence interval using a parameter that JMP generates (covariance and so on).
n = 500;
gamma = 1; //Ratio
t_dist = t Quantile( 1 - 0.025, n - 2 );
s_yy = 1.641302 ^ 2; //Variance of Y
s_xx = 1.336159 ^ 2; //Variance of X
s_xy = -0.16487; //Covariance of X and Y
phi = 1 / 2 * ArcSine(
t_dist * (2 / Sqrt( n - 2 )) * Sqrt(
gamma * (s_yy * s_xx - s_xy ^ 2) / ((s_yy - gamma * s_xx) ^ 2 + 4 * gamma * s_xy ^ 2)
)
);
beta_hat = -5.68667; //Estimate of Slope
theta_hat = ArcTan( beta_hat / Sqrt( gamma ) );
lower_confidence = Sqrt( gamma ) * Tan( theta_hat - phi );
upper_confidence = Sqrt( gamma ) * Tan( theta_hat + phi );
Show( Eval List( {lower_confidence, upper_confidence} ) );
Show( theta_hat - phi );
When calculating a confidence interval, beta(slope) is calculated from theta (beta equals tan(theta)). Theta is described in the reference. When calculating a confidence interval with your example data, the value of theta is less than -pi/2. In this case, a lower confidence interval (32.44) is greater than an upper confidence interval (-2.51), which is not reasonable. I think this is why JMP doesn't display a result.
Another approach is to use boostraping. Please see https://www.jmp.com/support/help/en/16.2/#page/jmp/example-of-bootstrapping.shtml#.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
Ahhh okay got it. That makes sense, thanks so much for your help @yuichi_katsumur !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
How to run this script? I clicked ‘run script’ and nothing happened.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
The results from the calculations are displayed in the log
Eval List({lower_confidence, upper_confidence}) = {32.4416248890056, -2.51129052017963};
theta_hat - phi = -1.6016111662264;
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Missing confidence intervals from orthogonal regression
Thank you very much. I don't know why LC is larger than UC, it feels very strange.
Recommended Articles
- © 2025 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us