- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Minitab and JMP: different results for CPK in Lognormal data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Minitab and JMP: different results for CPK in Lognormal data
Dears,
in this moment I'm evaluating a set of data.
This data are lognormal distributed.
I perform the CPK analysis wiht JMP and with Minitab: the capability resutl is different.
Some one of you, knonw the reason?
I think it could be linked to the type of formula usage for capability calculation... but I'm not sure.
Thanks in advance for the feedback.
Best regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Thanks for the feedback Dave.
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
I think that the key to understanding these methods and their differences is this statement from the cited JMP documentation: "However, unless you have a very large amount of data, a nonparametric fit might not accurately reflect behavior in the tails of the distribution."
So this situation is similar to reliability analysis. Most of the time in an analysis, the model is used for interpolation, but in reliability and capability, the emphasis is on extrapolation into the tails. The tails of the distribution are where the desired information resides. The parametric fit is more efficient (more information from less data). It is possible (i.e., sometimes) to fit a good parametric model (good estimates of the parameters) with only a handful of observations. This approach emphasizes the importance of your choice for the model and your belief in it.
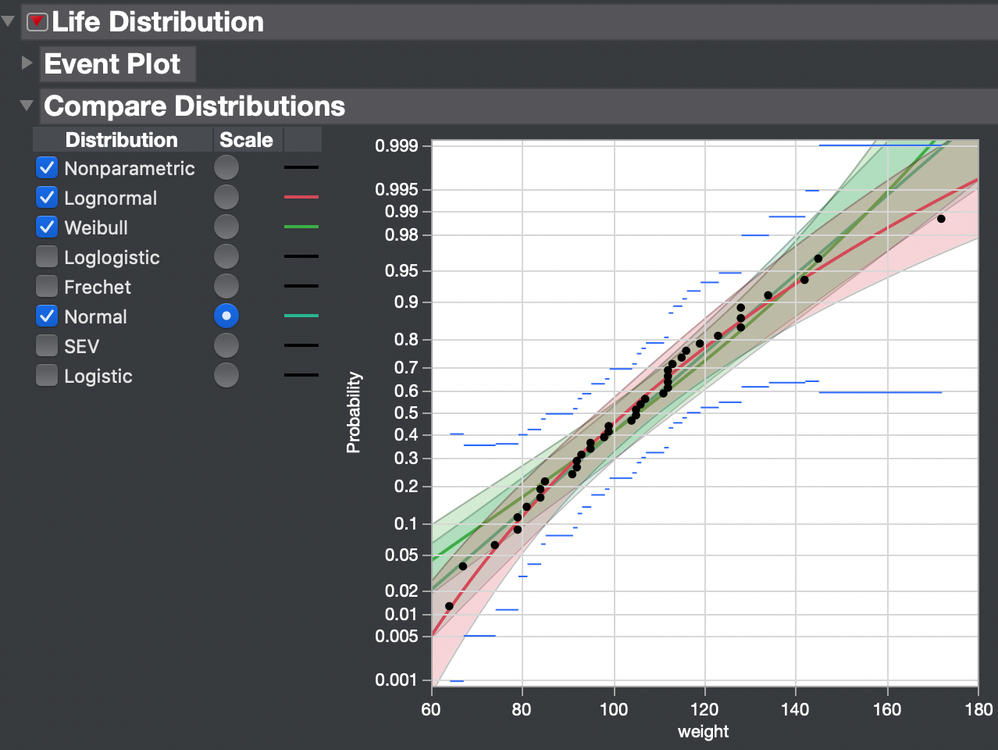
For example, I fit several distribution models to the weight data in Big Class using the Life Distribution platform for illustration.
I chose the Normal scale to linearize the CDF in this case. The models are very similar over the range of probability from 0.3 to 0.9. They are practically indistinguishable in this range and all of them provide similar estimates by interpolation. What about the tails, though? Calculating the capability requires estimating the weight range of ±3σ, which on the normal scale corresponds to probabilities (1.0 - 0.9973) / 2 = 0.00135 and 1 - 0.00135 = 0.99865. These different models will give very different extrapolations of weight at those probabilities.
The symmetric normal distribution equates the mean and the median. Only the median is guaranteed to represent the center in a non-normal distribution. So the Percentile method is a direct translation of the capability indices.
The Z Score method instead translates the specifications to quantiles but this transformation will still depend on the choice of the model and extrapolation. The specification is first converted to a probability with the fitted distribution model. Then the probability is converted to a quantile from the standard normal distribution, so it can be compared to ±3.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Thanks Mark clear explanation.
As you can image, when we speak with some organizations/customer... the question is very "practical question": you have lognormal distribution... which is the Cpk value? And... it is not so easy to pass the message that you can have different Cpk according the methodology you use for the calculation.
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Yes, I can appreciate the confusion as a JMP instructor!
That is why it is important for the customer to understand first what capability and performance indices are and second that there is more than one way to estimate them. If they ask for such indices, then they should have an idea about which way is best for them. Some industries have standards. Other industries and companies choose their own way. If the indices are to be used as important management data, then it is important for management to decide. They learn to understand and use complex financial data, indices, and calculations. Process information is no different.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Mark is completely correct. There are a lot of papers on the subject.
Fred Spiring, Bartholomew Leung, Smiley Cheng and Anthony Yeung, Bibliography of Process Capability Papers,QUALITY AND RELIABILITY ENGINEERING INTERNATIONAL Qual. Reliab. Engng. Int. 2003; 19:445–460 (DOI: 10.1002/qre.538)
lists many of the papers on the subject.
Here is another with a good summary of issues:
http://www.stats.uwaterloo.ca/~shsteine/papers/cap.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Thanks!
Best Regards,
Simone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minitab and JMP: different results for CPK in Lognormal data
Simone is raising a very legitimate point. If for example, I look at the link provided by @statman then it states the common requirement of Ppk > 1.33, but then goes on to say that "process capability indices calculated from non-normal processes are not comparable with those from normal processes".
I've always tended to favour the ISO/Percentile method for generalising capability indices for non-normal distributions. The reason being, for me the mathematics is a logical extension of the original intent for the indices.
But as I work more with vendors within supply chains I see that the capability indices tend to be used as generic performance indicators, and often combined to form a decision matrix to prioritise engineering actions. Ppk (or Cpk, take your pick - that's a separate discussion!) are used as a proxy measure of non-conformance. On this basis it is better to generalise the capability index such that it can be interpreted reasonably independent of the underlying distribution type. I believe that is the underlying basis of the Z-score method; therefore I'm tending to think now that this is the preferable method of calculation.
There is a 3rd approach used by some quality practitioners, which is to transform the data e.g. box-cox transformation; I believe it is the case (I still need to double-check this) that if you transform the data (and specs) and perform process capability then you will get the same outcome as if you used the Z-score method of calculation; which is another argument in its favour.
ps: the original title of the post was a query of Minitab versus JMP. Both systems support both the ISO/Percentile method and the Z-score method. But whereas Minitab defaults to the Z-score method, JMP defaults to the ISO/Percentile method. In JMP, you can change the default behaviour by selecting File>Preferences>Platforms.
- « Previous
-
- 1
- 2
- Next »
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us