- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: Minimum sample size question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Minimum sample size question
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
try this:
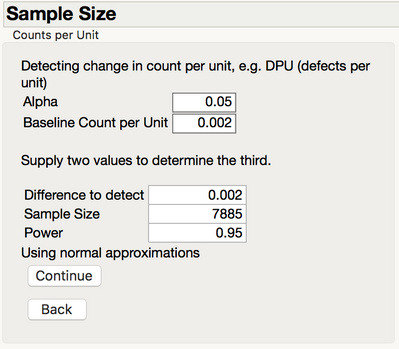
to get to the platform from the main menu: DOE >> Sample size and power >> Counts per unit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
try this:
to get to the platform from the main menu: DOE >> Sample size and power >> Counts per unit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
Thanks Ron!
From the calculations, I would need 7885 samples to get at least 1 defects at a 95% C.I.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
you are welcome @cal_Iim
if this an academic exercise than alpha of 0.05 and power of 0.95 are in place. if on the other hand you need to actually do this to save money in a production scenario i would choose these values based on cost/ benefit. for that you need to know how much does each fault cost to the firm.
in most production cases i came across, 0.05 was very far from optimal (too high or too low).
best,
ron
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
Cool! Can you give scenarios whereby the alpha of 0.05 was too high or low?
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Minimum sample size question
just think of the following.
if you are producing airbags for cars your company will go bankrupt quite quick if 5 out of 100 do not open when needed. you would need a much smaller rate of faults (or find a source of money to pay the compensation). on the other hand, if you produce something cheap and will not need to compensate unsatisfied customers and it is cheaper to produce more faults than why not?
same as with the power. you need to multiply the cost of each fault in $$$ by the probabilities and ask the economist in the team what can the company tolerate. just be careful he doesn't multiply everything by his personal bonus instead of company profit to determine policy. that was and perhaps is the common practice in mortgage banking. hahahah
hope i was clear.
ron
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us