- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Meaning of the parameter estimates
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Meaning of the parameter estimates
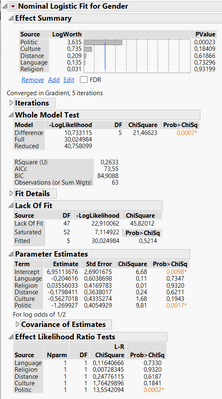
I am studying what discourages men and women from working in another country. I have my table and I can conclude that women are more discouraged by political factors than men with a significance level of 0,0017. But I am not entirely sure that I understand the "Estimate". What can I say about the -1,2699?
The score is a ranking of how a factor discourage desire to live and work in that country. From 1 - I does not discourage me, to 5 - It will very much discourage me.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Meaning of the parameter estimates
It looks you fit a binary logistic regression with several continuous factors. So, each estimates measures the log odds ratio (aks logit) of a factor. For example, for Politic, it shows that a one unit increase in Politic leads to a decrease in log odds ratio by 1.2699. A more widely used measure is odds ratio, which can be requested in JMP
http://www.jmp.com/support/help/13/Odds_Ratios_Nominal_Responses_Only.shtml
Some additional online resources on logistic regression parameters:
https://www.unm.edu/~schrader/biostat/bio2/Spr06/lec11.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Meaning of the parameter estimates
It looks you fit a binary logistic regression with several continuous factors. So, each estimates measures the log odds ratio (aks logit) of a factor. For example, for Politic, it shows that a one unit increase in Politic leads to a decrease in log odds ratio by 1.2699. A more widely used measure is odds ratio, which can be requested in JMP
http://www.jmp.com/support/help/13/Odds_Ratios_Nominal_Responses_Only.shtml
Some additional online resources on logistic regression parameters:
https://www.unm.edu/~schrader/biostat/bio2/Spr06/lec11.pdf
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Meaning of the parameter estimates
You using the Nominal Logistic Fit platform. You say that the response has five levels. If that is true, then you would have a different report. Does the column with the response really have five levels (1-5)? Is it using character or numeric data type? Is it using the ordinal modeling type? Such a response is ordinal in nature so you can take advantage of the extra information about rankings as well as differences. This arrangement should automatically lead to the Ordinal Logistic Fit platform (starting with Analyze > Fit Model).
The parameter estimate is coefficient of your linear predictor. So it represents the change in the response if you have a particular level of a categorical predictor or a change of 1 unit for a continuous predictor. It means the same thing as in a multiple regression analysis with a continuous response.
The difference here is the response. It is continuous through a transformation: the logit. You are fitting the linear predictor to the log( odds ). The ordinal response uses the cumulative logit, so you are fitting the linear predictor to the log( Pr( level i or below ) / Pr( level i+1 or higher ). In your case you will have four logits (the number of logits is always one less than the number of response levels). In effect, you have four sets of parameter estimates but they use a common intercept in the case of an ordinal response.
You can observe the explicit form of the ordinal logistic regression model by selecting Save Columns > Prediction Formula and then examining the data table. You will have one column for the linear predictor and then the back transformation for the probability of each level. Finally, you will have the prediction, which is the level with the highest probability.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Meaning of the parameter estimates
@Mark_Bailey Mark I hope you don't mind me jumping on this very old thread to ask you to clarify something. If my continuous predictor is a ratio (continuous from 0 to 1) then what constitutes a change of 1 unit of my continuous predictor? Is it the change from 0 to 1?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Meaning of the parameter estimates
Yes, one unit change in a continuous predictor always means a difference in predictor levels of 1. A change from 0 to 1 is such a unit change. Regression does not differentiate between an interval predictor and a ratio predictor.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us