- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: MANOVA repeated measures, two factors, multiple comparisons
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
MANOVA repeated measures, two factors, multiple comparisons
Hi,
I'm having trouble finding the right way to get the results I need.
I have done and experiment on 20 subjects (data for #6 is missing). We have 5 sample times. There are patients who had complications and those that didn't. We have the data normalized by the 1st sample which was defined as "1". See attached data.
1) If I use the one way model doing "sample" (i.e. 1 to 5) vs NL1st (the column with the results), I get the overall model and I get the comparisons between the different sampling times (see the script in the data table). But it is not repeated measures, and it doesn't have the option to compare between those with and without complications. Note that I used both parametric and non-parametric tests because the assumption of normality in this case is suspect.
2) Thus, I should use MANOVA (I don't want to use a linear model). I transposed the data - see attached. But i'm getting lost in the details of how to run it, even after spending a couple of hours going over the support literature, and part of my problem is how to interpret the results provided, where do I find the answer to my question. I know statistics enough to understand my problem and the solutions needed, but I feel JMP takes it to a much higher level so I get a bit lost sometimes in all of the verbose output. As I said, I need the three outputs detailed below, and if someone could hand-hold me going over this i'd be very grateful:
a) Are there differences between the different sampling times as a whole? If I understand correctly the way JMP works, it should be the f statistic for between groups for the "time" variable that JMP defines, right? (the groups are the 5 sampling times, not the 19 patients). If I understand correctly, the significance of the intercept is not of interest, right?
b) If so, then do a comparison between the different sampling times to see where those differences are, i.e. using Tukey or Scheffe (or something else that JMP offers). I don't understand what is the results obtained when I check "test each column separately also" - what method is it using? As above, if I understand correctly, the significance of the intercept is not of interest, right?
c) Separate the whole sample into those with and without complications, and compare them to see if there are significant differences between those with and without complications. In this case I don't care about which samples are the ones giving the differences, only if there are differences overall.
thank you very much,
Uriel.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA repeated measures, two factors, multiple comparisons
Hi @utkcito,
I'm confused why you say this isn't a repeated measures situation. Are you saying that because the data is longitudinal? Longitudinal data are repeated measures data. Often, you model longitudinal data with something like an AR(1) covariance structure. You can probably treat it as a fixed effect if you want to though.
I don't think you want to do MANOVA. The "M" in MANOVA refers to multiple responses, not multiple factors. It looks like you just have the 1 NL 1st response.
You could answer your questions all at once using Fit Model. I know you said you didn't want to use a linear model, but I don't think you can model this data properly without one. For starters, you need to make patient a random effect. Also, if you want to assess the impact of Complications, you really ought to just make that a factor in the model so you can test the signficance simultaneously with Sample.
I agree your data is not normal. It looks like a log transform on NL 1st takes care of that.
See the Fit Model script in the attached table. Here are the answers to the 3 questions you had:
1. Is Sample (time) significant? Answer: Yes. See the Fixed Effect Tests section of the Fit Model. The F-test has a p-values = 0.0025.
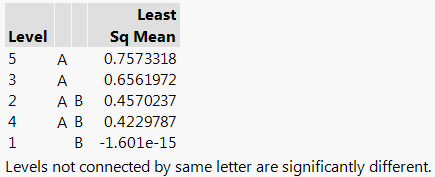
2. If so, which times are different? Answer: Tukey Analysis shows that time 1 is significantly different from 3 and 5. No other differences are significant.
3. Does complications have an effect? Answer: No. The Complication main effect is not significant, and neither is the Sample*Complication interaction. The interaction would indicate if the sampling time effects differ for patients with and without complications. There is not strong evidence that this is the case. See the Fixed Effect Tests for that as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA repeated measures, two factors, multiple comparisons
Hi @utkcito,
I'm confused why you say this isn't a repeated measures situation. Are you saying that because the data is longitudinal? Longitudinal data are repeated measures data. Often, you model longitudinal data with something like an AR(1) covariance structure. You can probably treat it as a fixed effect if you want to though.
I don't think you want to do MANOVA. The "M" in MANOVA refers to multiple responses, not multiple factors. It looks like you just have the 1 NL 1st response.
You could answer your questions all at once using Fit Model. I know you said you didn't want to use a linear model, but I don't think you can model this data properly without one. For starters, you need to make patient a random effect. Also, if you want to assess the impact of Complications, you really ought to just make that a factor in the model so you can test the signficance simultaneously with Sample.
I agree your data is not normal. It looks like a log transform on NL 1st takes care of that.
See the Fit Model script in the attached table. Here are the answers to the 3 questions you had:
1. Is Sample (time) significant? Answer: Yes. See the Fixed Effect Tests section of the Fit Model. The F-test has a p-values = 0.0025.
2. If so, which times are different? Answer: Tukey Analysis shows that time 1 is significantly different from 3 and 5. No other differences are significant.
3. Does complications have an effect? Answer: No. The Complication main effect is not significant, and neither is the Sample*Complication interaction. The interaction would indicate if the sampling time effects differ for patients with and without complications. There is not strong evidence that this is the case. See the Fixed Effect Tests for that as well.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA repeated measures, two factors, multiple comparisons
Also, I don't understand why MANOVA doesn't apply, in JMP at least that is the 1st platform they suggest for repeated measures, regardless if it is only one factor or many. In any case, this raises the question whether there is an option to do the ANOVA platform (i.e. "one way") in some way that does include repeated measurements? In theory there is I think, I just don't know if there's an implementation in JMP pro.
Thanks,
Uriel.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA repeated measures, two factors, multiple comparisons
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: MANOVA repeated measures, two factors, multiple comparisons
Please see this note in the JMP knowledge base.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us