- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: JMP Simulate Responses feature for binomial data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
JMP Simulate Responses feature for binomial data
Hello!
I want to simulate responses using built in JMP Simulate Responses feature.
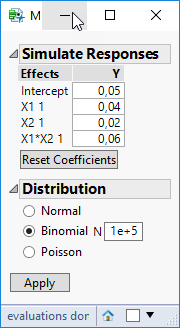
I use binomial distribution and my model for simplisity lets say is
p = 0,05 + 0.04*X1 + 0,02*X2.
(Actually I want to use simulation for fractional factorial designs.)
So
| X1 | X2 | Y |
| -1 | -1 | 0.05 |
| -1 | 1 | 0.02 |
| 1 | -1 | 0.04 |
| 1 | 1 | 0.06 |
In order to simulate this model what values do I need to enter in a Simulate Responses dialog box? Do I need to enter betas? But how do I derive them from coefficients?
Do I need to modify the formula?
Random Binomial( 100000, 1 / (1 + Exp( -1 * (0.05 + Match( :X1, "-1", 0.04, "1", -0.04, . ) + Match( :X2, "-1", 0.02, "1", -0.02, . ) +Match( :X1, "-1", Match( :X2, "-1", 0.06, "1", -0.06, . ), "1", Match( :X2, "-1", -0.06, "1", 0.06, . ), . )) )) )
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
This discussion might help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
Hi @gustavjung,
Just to be clear, the linear portion of the a logistic regression model does not directly output probabilities, but the log-odds. You need to apply the sigmoid (logistic) function (1/(1+exp(-x))) to convert log-odds to probabilities. That's why the function you posted is 1/(1+e^(-(beta0 + beta1*x1 + beta2*x2 + beta3*x1*x2))).
Coefficients are the betas. You should input 0 for x1x2 since your desired model has no x1x2 interaction.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
Thank you very much for your help!
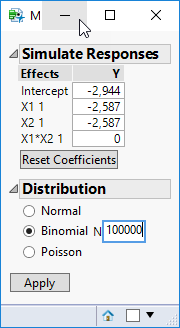
So now I understand that beta is calculated as folows:
p = 0,05 + 0.04*X1 + 0,02*X2.
Intercept (when all levels at -1 is 5% success rate)
is
ln(0,05/1-0,05) = -2,944
X1 (at -1 change from 0.05 to 0.09 at +1) which is 80% uplift
This is the same as saying that it is an uplift of 40% versus the average response for both levels of the factor.
Which means p = 0.05-40% versus p = 0.05+40%.
p = 0.03 versus 0.07
Which means log odds for X1 = ln( 0.07 / 1-0.07) = -2,587
For X2 (at -1 change from 0.05 to 0.07 at +1) which is 40% uplift
p = (0.05-20%)=0.04 versus (0.05+20%)=0.06
Which means log odds for X1 = ln( 0.07 / 1-0.07) = -2,752
So I enter this values to Response Simulator
When I analyze the simulated data in Generalized Linear Model
I get different prediction responses from that I was expected
Could you please point me on my mistakes?
I have attached the project file if needed.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
Hi,
I think the problem might be that the intercept is not where all Xs are at -1. Rather, I think the intercept is where all Xs are at 0.
I haven't checked this but you might want to take a look and see if that makes sense.
Phil
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
Hi @gustavjung,
JMP parameterizes linear models a bit differently than what most people are used to. The intercept is the average response (i.e. log-odds) across all factors, so as @Phil_Kay pointed out, it's actually when the values of X1 and X2 are 0.
If you want P( y = 1 | x1 = -1 & x2 = -1) = 0.05, then you need to basically need to input any combination of beta0, beta1, and beta2 such that beta0 + beta1*(-1) + beta2*(-1) = -2.944. Obviously, there's infinite solutions, so just plug in whatever you want for 2 of the betas and solve for the last.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
Hi @cwillden,
Thank you very much for the clarification!
But how do I calculate b1 and b2 if I have calculated b0?
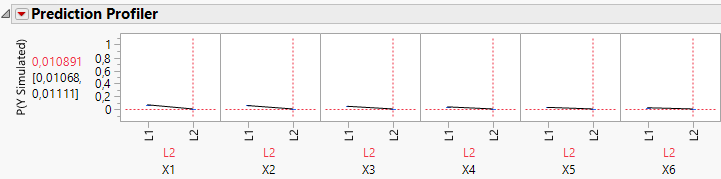
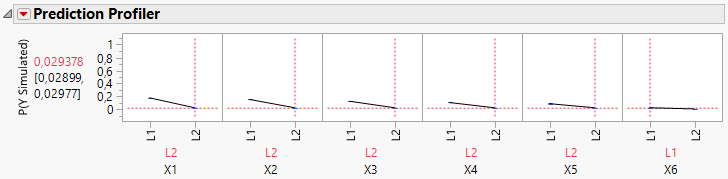
Also I have tried to reproduce this simulation from help site:
https://www.jmp.com/support/help/14/conduct-prospective-power-analysis-for-a-nonline.shtml
However, I couldn't get those numbers in prediction profiler:
Factor | Percent Passing at Xi = 1 | Percent Passing at Xi = -1 | Difference |
X1 | 73.11% | 26.89% | 46.2% |
X2 | 71.09% | 28.91% | 42.2% |
X3 | 69.00% | 31.00% | 38.0% |
X4 | 66.82% | 33.18% | 33.6% |
X5 | 64.56% | 35.43% | 29.1% |
X6 | 62.25% | 37.75% | 24.5% |
In Prediction Profiler
X6 at -1 is 0.010891
X6 at +1 is 0.029
How does it correspond to initial values?
X6 | 62.25% | 37.75% | 24.5% |
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: JMP Simulate Responses feature for binomial data
While you might set the random seed for generating the design, that doesn't apply to simulating responses. Therefore, you are going to get different results in your fitted model to the simulated data. If you look at the parameter estimates, they should very roughly correspond to the coefficients you inputted into the simulation.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us