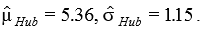Is there a way to automate/script the Winsor process of outlier filtering?

[#1]

Is there a way to automate/script the Winsor process of outlier filtering? I found the two addins from Brady, but those do not exclude the  outlier rows, they only pertain to the enhancing the Summary function.

Imputation Addin

Extended Summary Add-in

[#2]

Your question confuses me.  Winsorising outliers is generally defined as setting the extreme values to a specified percentile, not excluding them.  It is analogous to clipping in signal processing.  Excluding outlier rows is generally not Winsorising.

That said, any algorithmic approach your heart desires can be scripted.  If you write a script to do it, use matrices.  They run a whole lot faster, especially with large datasets.

[#3]

Most all actions in JMP can be scripted by going to the red triangle and go to SCRIPT > COPY SCRIPT

This way you can glue together these bits of scripts into a larger automated program.

This is true for every JMP action/function, etc.... with the EXCEPTION of the Robust Outlier Filter function under:

COL > MODELING UTILITIES > EXPLORE OUTLIERS    

I want to automate the Huber filter with K=3 on a given set of parameters.  I will do this over and over again.

I want to automate it to ease my workload.

[#4]

In general, it's considered poor taste and bad practice to filter outliers without knowing the cause.  Even when a cause is known, using a filtering criteria that doesn't apply to your data set will introduce even more error than just leaving the outliers in the dataset.  Important questions need to be asked, is the data symmetric? skewed? normal? is there any masking?  Is your data set really two different distributions?  Would splitting them be better?  It's impossible to really know your data without actually looking at it.  Automating outlier filtering will lead to false conclusions.  Just as bad a practice as "p-hacking".

Of course, this doesn't mean there aren't reasons to automate a process.  For example, using an outlier filtering criteria to automate updating control limits on a control chart where the data is viewed/monitored over a course of time.

If you want to automate it, you'll need to write the script.  You can see http://www.rsc.org/images/robust-statistics-technical-brief-6_tcm18-214850.pdf for some more information on what the Huber Method is actually doing.  Hope this helps.

[#5]

To CHFields​:  I understand better now.  That is not the ONLY robust procedure that's not easily scriptable!  The Robust Means and Robust Standard Deviation from the Distribution platform are not functions available to JSL either.  Please see last year's Christmas List for Santa...

To msharp​: When I asked JMP for a reference for the Robust Mean and Robust Standard Deviation, the developer directed me to Huber, P.J.(1973); "Robust Regression: Asymptotics, Conjectures, and Monte Carlo"; The Annals of Statistics, Vol 1, No. 5, pp799-821, which detail procedures substantially different from the reference you quoted.  Peter Huber is a titan of Robust Statistics, and his more modern books on the subject (Robust Statistics 2004) sing the praises of M estimates (which the Annals paper also detailed), so I don't know if JMP is really doing the Winsorizing you reference.  Is it really?

Huber M estimates don't look like they would be too fun to script from scratch.  Hence the Christmas List request.

[#6]

There are many ways to calculate Robust Mean and Robust Standard deviation.  The article I reference shows how to calculate the median (by definition is a robust mean) and MAD(robust standard deviation).  These are the most basic.  However, any metric that calculates the center and spread and is resistant to change due to outlier data can be considered a robust mean or robust std dev and there are certainly more complex algorithms than the median/MAD approach.

The reason I chose to share that article is because it shows the basics to the Winsorizing process using the easy to understand median/MAD.  If I was going to program the process from scratch I'd start here.

I'm not a JMP programmer so I don't know the actual method they use; but I doubt they use the method described in that paper.  That paper really is just helpful to understand the basics.  The paper itself states most the flaws, one that stands out most to a programmer is the slow convergence.

[#7]

I followed the Huber method described in the AMC paper that msharp link to.  Scripting it wasn't too bad, the hard part is knowing if I've interpreted the algorithm correctly.  It would seem that as I iterate through (say N times) and update the data array with a new mean-hat +/- 1.5 x sigma-hat value, that for the ith iteration I would use the data array from i-1 but this doesn't work for me. I get better results by always updating the original data (i=0) while using updated mean-hat and sigma-hat.  Better results but seems wrong. Does anyone have experience implementing this algorithm?

Incidentally, according to this page (The Distribution Report), JMP's robust mean / standard deviation in the distribution platform is using Huber M-estimation, but I'm not sure how they are windsorizing. My script produces similar results in some cases, and not so similar in others. But as I stated above I'm not sure if I'm doing it correctly.

Thanks,
Mike

[#8]

Here's my quick code following the paper exact:

//Data Set in Paper

x = [4.5,4.9,5.6,4.2,6.2,5.2,9.9];

//Determine Median and Robust Sigma (MAD)

mean = quantile(.5,x);

y = abs(x - mean);

MAD = quantile(.5,y);

sigma = MAD*1.5;

sigmaold = 0;

//Converge

while(abs(sigma - sigmaold) > 2e-16,

  for(i=1,i<=nrows(x),i++,

  if(x<mean-1.5*sigma,

  x = mean-1.5*sigma

  );

  if(x>mean+1.5*sigma,

  x = mean+1.5*sigma

  );

  );

  meanold = mean;

  sigmaold = sigma;

  mean = mean(x);

  sigma = 1.134*std dev(x);

);

//Evaluate

print(x);

[#9]

That is essentially what I had, although i had everything in array format so i could inspect the data for each iteration. Yours is cleaner, so I hope you don't mind I've modified it a bit. I replaced the for() loop with the Loc function as it might be more efficient in case anyone else is using this for large data sets. (Disclaimer, I've used this function only once or twice... hopefully it is the right choice.)

When I ran  your function and mine, I found that it converged in 1 iteration with a mean of 5.339 and a sigma of 1.044. The paper seems to indicate it would take several iterations. I thought they meant even for this data set but maybe they were generalizing. They go on to say that the Huber estimated mean is 5.36 and sigma is 1.15. I was not able to reproduce that estimated mean, but when I replaced 'x' data with x_orig (original data) in each iteration, I got a mean of 5.386 and sigma of 1.1459.  You can see the line in the code below to enable / disable this. This doesn't really feel like the correct way to iterate something, but I'm not really sure where I've gone wrong in being able to compute this. Forgive the sig digits errors but I wanted to show more about the variable contents here.

From the paper:

names default to here(1);

clear log();

//Data Set in Paper

x_orig = [4.5, 4.9, 5.6, 4.2, 6.2, 5.2, 9.9];

x = [4.5, 4.9, 5.6, 4.2, 6.2, 5.2, 9.9];

//Determine Median and Robust Sigma (MAD)

mean = Quantile( .5, x );

y = Abs( x - mean );

MAD = Quantile( .5, y );

sigma = MAD * 1.5;

sigmaold = 0;

//Converge

While( Abs( sigma - sigmaold ) > 2e-16,

      //x = x_orig;                                   // try turning this on / off

      x [Loc(x > (mean + 1.5 * sigma))] = mean + 1.5 * sigma;

      x [Loc(x < (mean - 1.5 * sigma))] = mean - 1.5 * sigma;

      meanold = mean;

      sigmaold = sigma;

      mean = Mean( x );

      sigma = 1.134 * Std Dev( x );

      show(mean, sigma);

);

Thanks,
Mike

[#10]

Yes, yes.  We'd want to run the winsorization process on the original data set with the adjusted mean and sigma changing.  Adding the x=xorig is correct.  Like I said I coded it quickly.

As for matching the paper:

Since the data set has only 1 degree of freedom (what value to approximate the outlier) both sigma and mean are fixed based on the winsorization.  Given this fact there's no way to get a mean of 5.36 AND sigma of 1.15.  5.386 and 1.145 rounded to the second digit would yield 5.39 and 1.15. Thus, my best guess is that this is a simple typo, and not a mathematical error.  Given the correctness of the paper up to that point, and it coming from the Analytical Methods Committee from the Royal Society of Chemistry I'll give them the benefit of the doubt.