Is a mixture design required for a two component mixture?

[#1]

I have a question about a mixture design that I am working on. The experiment in question is looking at the effect of blending different types of fluids on material compatibility.

Factors

Fluid_1 treat rate - the fraction of fluid A - 0-100

Fluid_2 treat rate - the fraction of fluid B - 0-100

Fluid_1 type - categorical, two levels

Fluid_2 type - categorical, two levels

Response

swell - continuous 

A complication in the design stage is that the type of fluid A used cannot have an effect on the response when Fluid_A treat rate is 0, the same is true for Fluid_B at 0 treat rate. I therefore set up the design to exclude Fluid_A and Fluid_B type unless crossed with the relevant treat rate factor. This is reasonable provided that the option to centre polynomials is unchecked when fitting the model. I also wanted to put in some restrictions so that eg only one Fluid_A type would be used at Fluid_A treat rate of <10. The two runs in the below table are essentially repeats, but JMP will not treat them as such, including restrictions avoids this.

Fluid_1_treat	Fluid_1	Fluid_2
0	A	A
0	B	A

Such restrictions are not allowed in a mixture deisgn, however since this is only a two component mixture with A always depending on B I opted to exclude Fluid_2 treat rate and simply use the treat rate of Fluid_1 as the only continuous factor. I therefore end up with a design for the following model.

Fluid_1_treat

Fluid_1_treat x Fluid_1

Fluid_1_treat x Fluid_1_treat

Fluid_1_treat x Fluid_2

Fluid_1_treat x Fluid_1_treat x Fluid_1

When fitting this I can produce a good model, however it has the Fluid_1 type affecting the response at 0 treat rate (see prediction profiler 1), which is not physically possible. Also the treat rate at which there is no effect of the Fluid_1 type is 50% (see prediction profiler 2), which seems rather too round a number to be a real result.

Fitting it as a mixture I results in a more sensible model,

Fluid_1_treat (mixture)

Fluid_1_treat x Fluid_1

Fluid_1_treat x Fluid_2_treat

Fluid_1_treat x Fluid_2

Fluid_2_treat (mixture)

Fluid_1_treat x Fluid_2_treat x Fluid_1

However there are some quite high correlation coefficients when the final model effect (Fluid_1_treat x Fluid_2_treat x Fluid_1) is included. Augmenting the design is necessary to resolve this. Is this because having the two mixture factors in the model I effectively have an additional effect to fit, despite the fact that it is linearly dependent on the other mixture factor?

Obviously the simple solution is to do the extra runs for the mixture design, but can anyone help me understand the issues with the first model?

[#2]

Would it work to replace the fluid rate fraction factors with a single factor that is a ratio of A to B. This keeps the A and B levels correlated like in a mixture.

[#3]

Alternatively, you could include only one of the components as a continuous factor with an appropriate range in the design. You can then add a data column after you click Make Table to compute the proportion of the other component to achieve the appropriate sum (e.g., 1). However, you should not include the second component in the model.

[#4]

@Mark_Baileyyes, that was my solution initially. I then took the steps discussed here of removing the "coding" property of the column and unchecking centre polynomials in the fit model platform. However, doing that results in a model that has the response dependent on the type of a fluid when that fluid is not present (prediction profiler 2) in my original message. This is despite ensuring that the fluid type does not appear in the model as a main factor, it only appears when crossed with the treat rate. 

Not taking the steps of removing coding I get a model which makes some more sense, however there is a singularity which necessitates removal of the Fluid_1_treat x Fluid_1_treat x Fluid_1 factor from the model and the correlation matrix starts to look rather ugly. The DoE was set up to include this in the model so I assume something to do with the analysis set up has caused the problem here?

I don't have the singularity issue when fitting as a mixture, but still run into high correlations.

[#5]

I think you do not need the steps suggested by Phil because this solution avoids the problem in the first place. Coding factor levels and centering polynomials are generally best practices. They should be avoided only special cases, which this case is not.

Please show us the design you are using in this analysis, the original full model (so we know what are the terms), and the singularity report.

I notice a statement by you, "A complication in the design stage is that the type of fluid A used cannot have an effect on the response when Fluid_A treat rate is 0." I think that is handled in a natural way by the linear model you are using, without the need for a special design. The complicated modifications under discussion might not be necessary. (I'm not sure, though.)

[#6]

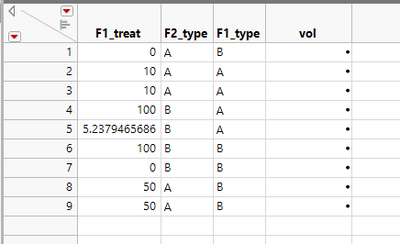
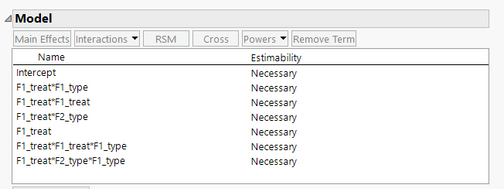
This is the code that is used to generate the design, and the design and model are shown below.

DOE(
	Custom Design,
	{Add Response( Match Target, "vol", ., ., . ),
	Add Factor( Continuous, 0, 100, "F1_treat", 0 ),
	Add Factor( Categorical, {"A", "B"}, "F2_type", 0 ),
	Add Factor( Categorical, {"A", "B"}, "F1_type", 0 ),
	Set Random Seed( 668463152 ), Number of Starts( 80 ), Add Term( {1, 0} ),
	Add Term( {1, 1}, {3, 1} ), Add Term( {1, 2} ), Add Term( {1, 1}, {2, 1} ),
	Add Term( {1, 1} ), Add Term( {1, 2}, {3, 1} ),
	Add Term( {1, 1}, {2, 1}, {3, 1} ), Add Alias Term( {2, 1}, {3, 1} ),
	Replicates( 2 ), Set Sample Size( 9 ),
	Disallowed Combinations(
		F1_treat >= 90 & F1_treat <= 100 & F2_type == "A" | F1_treat >= 0 & F1_treat
		 <= 5 & F1_type == "A"
	), Simulate Responses( 0 ), Save X Matrix( 0 ), Make Design}
)

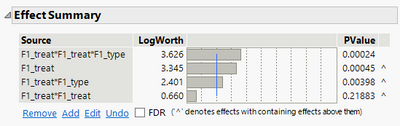
When I fit the model it I have the following significant effects

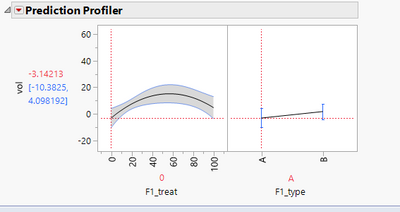
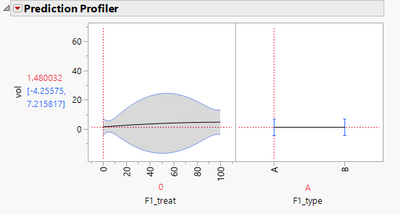
However, the prediction profiler has the response being dependent on the F1_type when F1_treat = 0. This is the part that I cannot understand, given that nowhere in the model does F1_type appear in the absence of F1_treat.

Removing both the coding and unchecking centre polynomials gives the below singularity report, but once one of the higher order terms has been removed gives a more sensible (scientifically at least) model where at F1_treat = 0 the F1_type has no effect on the response.

Regarding your final point about the design stage, I did it as otherwise the design seems to come up with a lot of runs which are essentially repeats but without understanding them as such. Should this be taken into account by the model factors included during the design?

I notice a statement by you, "A complication in the design stage is that the type of fluid A used cannot have an effect on the response when Fluid_A treat rate is 0." I think that is handled in a natural way by the linear model you are using, without the need for a special design. The complicated modifications under discussion might not be necessary. (I'm not sure, though.)

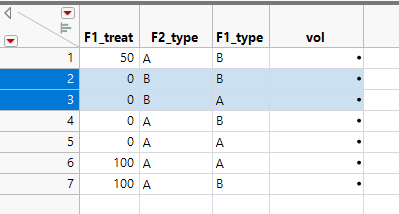
 For example, running the custom DoE tool with everything the same but with the restrictions removed and 0 repeats chosen the following design results. The highlighted rows are essentially repeats as at F1_treat = 0 then the F1_type can have no effect, the same is true of the two rows below those highlighted. Repeats are obviously no bad thing, I just use this as an example.

Many thanks for the help with this, and any further feedback