ICH Q1E expiration timepoint extrapolation for repeated measurements

[#1]

Dear All,

I check the below link for stability extrapolation based on ICH Q1E

https://www.jmp.com/support/help/en/17.0/index.shtml#page/jmp/stability-analysis-in-the-degradation-...

But, I have a concern for it. This example is for one measurement for each time point. However, pharmaceutical tests for instance assay analysis, we perform more than 1 measurement for each time point. Generally 3 measurements or based on investigation more than 3 will be performed. So, I would like to ask if we have multiple results for different timepoints, how can we perform extrapolation of them? do we need to calculate mean of each time point for extrapolation or can we use each individual results to calculate expiration time point.

Could someone clarify for it?

[#2]

Typically this stability analysis is performed on the Reportable Result for the time point.  Often the assay format, will include replicates, or even multiple runs with multiple replicates. The goal of taking repeated measures is to get a better estimate of the true value when there is noise in assay system.   All of the results aren't reported, only the mean of the replicates, which is the reported value for the specific sample. 

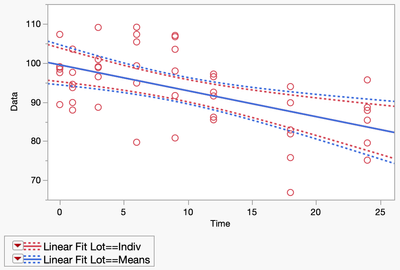
In the figure below I have 5 replicates for each time point and I've fitted a line to both the Individuals and the Means of each time point.

Note that the slope and intercept is the same.   (Its hard to see because the red and blue regression lines are right on top of each other.)

However, the confidence intervals aren't the same. The interval for the means (blue) is wider than individuals (red).   Why?  When we fit the individuals we get 39 degress of freedom (40 points -1), but when we fit the means, we only have 7 degrees of freedom (8 points -1).   

This has an impact on when the lower 95% confidence interval crosses the lower spec limit. The individuals will cross later than the means. (longer dataing with individuals than means).   I'm sure you're thinking, "Why would anyone use the means over the individuals?", that's a no brainer right!  There is a problem with this, some of the individuals from early time points might be below the lower spec limit, and that would cause some sever problems with releasing the product.   Since we acknowledge that the assay is really noisy (really typical of biologics) then when we take the mean of the replicates for the reported time point result, we avoid this problem. 

Also, each time point is one experimetal unit, and its nearly always appropriate to take the mean of replicate measure for one experimental unit. 

In the script attached below is an example generator for the figure above.