- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Hypothesis testing with censored data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Hypothesis testing with censored data
Hi,
I am trying to figure out how to do hypothesis testing with censored data and how to determine sample size for future studies.
My data are both left censored and interval censored. I want to show that an "event" has happened for 95% of samples before a certain timepoint (upper limit).
I have used the Life Distribution functionality in JMP to make an event plot, determine the best model for my data, and to determine at what timepoint 95% of my samples have shown an event. I then compare the timepoint for the 95% quantile to my upper limit. Does this sound like the correct approach?
I then want to use the model data from the study to determine the required sample size for my next study. Any suggestions on how to do that?
Kind regards
Thor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: Hypothesis testing with censored data
You are on the right track on using the 95% quantile estimate. In addition, the 95% quantile estimate is just a point estimate, it has uncertainties. The actual value that you may want to compare with is usually not that particular value, but the confidence bounds associated with it. But it depends on what your objective is. For example, if your objective is to find the quantity T that AT LEAST 95% of events occur before T, with a desired degree of confidence level L. Then you should look for the upper bound of the one sided confidence bound at confidence level L. Suppose the desired confidence level is 90%. This quantity T is the upper bound of the one-sided confidence bound at 90% confidence level. This quantity T is larger than the 95% quantile, so it takes uncertainties in estimation into account. And if your particular timepoint is LARGER than this quantity T, you may firmly claim that 95% of events occur before that timepoint. There are quite some inequalities here. It is all about being on the correct side.
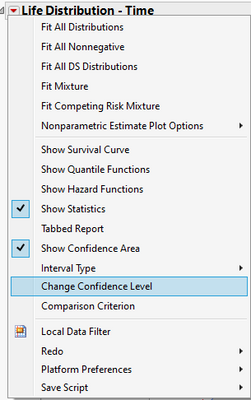
To find the number, you need to know where to specify the desired confidence level; see this screenshot:
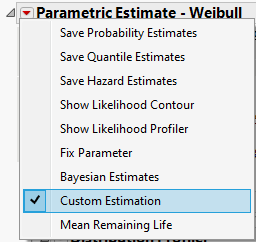
To find the one-sided confidence bound, you need to find "Custom Estimation":
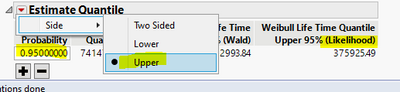
Within Custom Estimation, find the Quantile part, enter 0.95 for probability, choose "Upper" for Side. And use the "Likelihood", instead of "Wald" for your report, in case your sample size is not big.
For the sample size question, you may want to check out two places: Life Testing among Sample Size Explorers in JMP 17 or Reliability Test Plan among Sample Size and Power in JMP 17 and before. The latter is about to retire. They are both under DOE menu. The main point is: identify your objective, which should be one of two, and in your case, I guess that the objective is to estimate the quantile (the other is to estimate probability). Beside that, make sure finding sample size is the goal. Then specify the remaining information.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us