- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How to perform iterative DoE methods with Custom DoE Platform
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to perform iterative DoE methods with Custom DoE Platform
Hi,
I've read some posts in the past regarding methods of how to approach DoE and model refinement. One method I saw was to build onto models using the augment design option and it was described as an iterative process.
In this way, you would perform more of a screening type custom DoE in the initial stages, evaluate the model, reduce the model, then augment the design for further optimization and variance reduction.
1. Does this process seem sound as a method of approaching model refinement?
2. What steps would you take to refine your model using this method?
- Should the screening evaluate both main effects and interaction effects simultaneously or should you start with main effects and then follow-up with 2nd order interactions?
- If a main effect is found "insignificant" does this mean there is no potential for interaction effects as well?
- Should you add center-points to detect curvature at the screening phase?
- Should you add replicates at this phase? (I've heard this may be unnecessary when large impacts are being evaluated rather than low variance)
- When should replicates be added/focus toward variance reduction?
Thanks in advance!
- Tags:
- windows
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to perform iterative DoE methods with Custom DoE Platform
I'll give it a shot. Please excuse my "lecture".
There is no "one way" to build models. Some methods may be more effective or efficient given the situation, but it all depends on the situation. Let me also suggest, the model must be useful.
A good model is an approximation, preferably easy to use, that captures the essential features of the studied phenomenon and produces procedures that are robust to likely deviations from assumptions
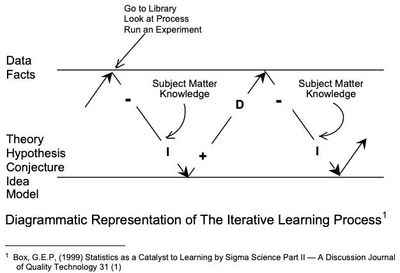
G.E.P. Box
I use Scientific Method (i.e., an iterative process of induction-deduction, examples include Deming's PDSA or Box's Iterative Learning Process) as a basis for all investigations.
The impetus or motivation (e.g., reduce cost, improve performance, respond to customer complaint, add function, etc.) should be stated, but care should be taken as this may simply be a symptom . A decision should be made as to whether this is a study to explain what is already occurring or is the study intended to understand causal structure (I am biased to understanding causality). In addition, it must be understood what the constraints are (e.g., resources, sense of urgency). Start with situation diagnostics (e.g., asking questions, observation, data mining (this may include different regression type procedures), collaboration, potential solutions, measurement systems, etc.). What are the appropriate responses? Is there interest in understanding central tendency, variation or both. Do the response variables appropriately quantify the phenomena? I have seen countless times where the problem was variation, but the response was a mean. That will never work.
Develop hypotheses. Once you have a set of hypotheses, get data to provide insight to those hypotheses. The appropriate data collection strategy is situation dependent. If there are many hypotheses or factors (e.g., >15), the most efficient approach may be to use directed sampling (e.g., components of variation, MSE) studies. The data should help direct which components have the most leverage. As the list of "suspects" becomes smaller, perhaps experimentation can accelerate the learning. This will likely follow a sequence of iterations, but the actual "best" sequence is likely unknown to start. Error on the side of starting with a large design space (e.g., lots of factors and bold levels). This will likely be some sort of fractional experiment over that design space. Realize, the higher order effects (e.g., interactions and non-linear) are still present, they just may be confounded. Let the data, and your interpretation of what the insight the data is providing you, be the guide.
Regarding Noise (e.g., incoming materials, ambient conditions, measurement error, operator techniques, customer use, etc.), I think this is the most often missed opportunity. Intuitively, I think our bias is to hold those untested factors constant while we experiment. This is completely wrong. This creates narrow an inference space and reduces the likelihood results will hold true in the future. Understanding noise is a close second to understanding a first order model. Think about the largest experiment you have ever designed,. Think about how many factors were in the study. What proportion of ALL factors is the experiment? Unfortunately, the software is not really capable of providing direction as to how to appropriately study the noise.
"Block what you can, randomize what you cannot", G.E.P. Box
Much is spent on the most efficient way to study the design factors (e.g., custom, optimality, DSD), but little is spent on incorporating noise into the study. I'm not sure what a complex model does for you if you are in the wrong place. Not sure it can be "automated" in a software program? it requires critical thinking.
Regarding your specific questions:
- Should the screening evaluate both main effects and interaction effects simultaneously or should you start with main effects and then follow-up with 2nd order interactions?
Advice is to develop models hierarchically. Your question might not be "evaluate" but estimate or separate? All depends on what you know and what you don't. Error on the assumption: you don't know much!
- If a main effect is found "insignificant" does this mean there is no potential for interaction effects as well?
Absolutely not. I give you F=ma (neither main effect, m or a, is significant)
- Should you add center-points to detect curvature at the screening phase?
Situation dependent. Are you suspicious of a non-linear effect? Why? Are you in a design space that the non-linear effect is useful?
- Should you add replicates at this phase? (I've heard this may be unnecessary when large impacts are being evaluated rather than low variance)
- When should replicates be added/focus toward variance reduction?
You need a noise strategy. Replication is one of many. Again the question will be is the noise in the design space similar to the noise near where you want to be? If so, study it now.
The exact standardization of experimental conditions, which is often thoughtlessly advocated as a panacea, always carries with it the real disadvantage that a highly standardized experiment supplies direct information only in respect to the narrow range of conditions achieved by the standardization. Standardization, therefore, weakens rather than strengthens our ground for inferring a like result, when, as is invariably the case in practice, these conditions are somewhat varied.
- R. A. Fisher (1935), Design of Experiments (p.99-100)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to perform iterative DoE methods with Custom DoE Platform
Thank you for such a thoughtful answer. It gives me a lot to consider moving forward in how I approach designs.
I do have some follow up questions. I'd like to find an efficient manner to minimize the number of runs required to refine a model of 9 continuous factors. We have a process that was created using non statistical methods, so we are now evaluating with JMP to ensure there are no surprises... The goal is to evaluate and remove insignificant components, then build an effective, predictive model within our design space. I work in purification, and there are finite responses (Recovery/purity). Because of this, it makes sense to me that each factor should have an optimum (A quadratic element) over a wide test range.
I think the general thought process is to perform a screen, remove insignificant factors (main effects and interactions), then focus on quadratics and variance reduction by augmenting the design.
- How do you know what interactions are important?
- I am working on buffer refinement and there are many components where we are unsure of interactions
- With custom application, if you assume all interactions must be evaluated, then the "screen" becomes very large (48 runs)
- How do you know what interactions are being evaluated when using non-custom screening options?
- If you rely on applications such as definitive screen, or classic screens, it is closer to 30runs
- I'm more uncomfortable with this option because I am unsure what interactions are being evaluated, and which aren't
Really, it seems that sorting the interactions effects are the bulk of the runs. I want to ensure I am doing this efficiently.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to perform iterative DoE methods with Custom DoE Platform
I'll give it a shot. Please excuse my "lecture".
There is no "one way" to build models. Some methods may be more effective or efficient given the situation, but it all depends on the situation. Let me also suggest, the model must be useful.
A good model is an approximation, preferably easy to use, that captures the essential features of the studied phenomenon and produces procedures that are robust to likely deviations from assumptions
G.E.P. Box
I use Scientific Method (i.e., an iterative process of induction-deduction, examples include Deming's PDSA or Box's Iterative Learning Process) as a basis for all investigations.
The impetus or motivation (e.g., reduce cost, improve performance, respond to customer complaint, add function, etc.) should be stated, but care should be taken as this may simply be a symptom . A decision should be made as to whether this is a study to explain what is already occurring or is the study intended to understand causal structure (I am biased to understanding causality). In addition, it must be understood what the constraints are (e.g., resources, sense of urgency). Start with situation diagnostics (e.g., asking questions, observation, data mining (this may include different regression type procedures), collaboration, potential solutions, measurement systems, etc.). What are the appropriate responses? Is there interest in understanding central tendency, variation or both. Do the response variables appropriately quantify the phenomena? I have seen countless times where the problem was variation, but the response was a mean. That will never work.
Develop hypotheses. Once you have a set of hypotheses, get data to provide insight to those hypotheses. The appropriate data collection strategy is situation dependent. If there are many hypotheses or factors (e.g., >15), the most efficient approach may be to use directed sampling (e.g., components of variation, MSE) studies. The data should help direct which components have the most leverage. As the list of "suspects" becomes smaller, perhaps experimentation can accelerate the learning. This will likely follow a sequence of iterations, but the actual "best" sequence is likely unknown to start. Error on the side of starting with a large design space (e.g., lots of factors and bold levels). This will likely be some sort of fractional experiment over that design space. Realize, the higher order effects (e.g., interactions and non-linear) are still present, they just may be confounded. Let the data, and your interpretation of what the insight the data is providing you, be the guide.
Regarding Noise (e.g., incoming materials, ambient conditions, measurement error, operator techniques, customer use, etc.), I think this is the most often missed opportunity. Intuitively, I think our bias is to hold those untested factors constant while we experiment. This is completely wrong. This creates narrow an inference space and reduces the likelihood results will hold true in the future. Understanding noise is a close second to understanding a first order model. Think about the largest experiment you have ever designed,. Think about how many factors were in the study. What proportion of ALL factors is the experiment? Unfortunately, the software is not really capable of providing direction as to how to appropriately study the noise.
"Block what you can, randomize what you cannot", G.E.P. Box
Much is spent on the most efficient way to study the design factors (e.g., custom, optimality, DSD), but little is spent on incorporating noise into the study. I'm not sure what a complex model does for you if you are in the wrong place. Not sure it can be "automated" in a software program? it requires critical thinking.
Regarding your specific questions:
- Should the screening evaluate both main effects and interaction effects simultaneously or should you start with main effects and then follow-up with 2nd order interactions?
Advice is to develop models hierarchically. Your question might not be "evaluate" but estimate or separate? All depends on what you know and what you don't. Error on the assumption: you don't know much!
- If a main effect is found "insignificant" does this mean there is no potential for interaction effects as well?
Absolutely not. I give you F=ma (neither main effect, m or a, is significant)
- Should you add center-points to detect curvature at the screening phase?
Situation dependent. Are you suspicious of a non-linear effect? Why? Are you in a design space that the non-linear effect is useful?
- Should you add replicates at this phase? (I've heard this may be unnecessary when large impacts are being evaluated rather than low variance)
- When should replicates be added/focus toward variance reduction?
You need a noise strategy. Replication is one of many. Again the question will be is the noise in the design space similar to the noise near where you want to be? If so, study it now.
The exact standardization of experimental conditions, which is often thoughtlessly advocated as a panacea, always carries with it the real disadvantage that a highly standardized experiment supplies direct information only in respect to the narrow range of conditions achieved by the standardization. Standardization, therefore, weakens rather than strengthens our ground for inferring a like result, when, as is invariably the case in practice, these conditions are somewhat varied.
- R. A. Fisher (1935), Design of Experiments (p.99-100)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to perform iterative DoE methods with Custom DoE Platform
Thank you for such a thoughtful answer. It gives me a lot to consider moving forward in how I approach designs.
I do have some follow up questions. I'd like to find an efficient manner to minimize the number of runs required to refine a model of 9 continuous factors. We have a process that was created using non statistical methods, so we are now evaluating with JMP to ensure there are no surprises... The goal is to evaluate and remove insignificant components, then build an effective, predictive model within our design space. I work in purification, and there are finite responses (Recovery/purity). Because of this, it makes sense to me that each factor should have an optimum (A quadratic element) over a wide test range.
I think the general thought process is to perform a screen, remove insignificant factors (main effects and interactions), then focus on quadratics and variance reduction by augmenting the design.
- How do you know what interactions are important?
- I am working on buffer refinement and there are many components where we are unsure of interactions
- With custom application, if you assume all interactions must be evaluated, then the "screen" becomes very large (48 runs)
- How do you know what interactions are being evaluated when using non-custom screening options?
- If you rely on applications such as definitive screen, or classic screens, it is closer to 30runs
- I'm more uncomfortable with this option because I am unsure what interactions are being evaluated, and which aren't
Really, it seems that sorting the interactions effects are the bulk of the runs. I want to ensure I am doing this efficiently.
Thanks!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to perform iterative DoE methods with Custom DoE Platform
Here are my thoughts. Unfortunately, I don't have a thorough understanding of your process, so please keep that in mind.
"I'd like to find an efficient manner to minimize the number of runs required to refine a model of 9 continuous factors."
Minimize in 1 experiment? Do you plan to iterate? What is the over-all experiment budget (e.g., time and resources)? The fewer the runs, the less degrees of freedom available to separate and assign effects.
"We have a process that was created using non statistical methods, so we are now evaluating with JMP to ensure there are no surprises."
Ultimately you want a predictive model that is useful and robust. How you arrive at the model may impact resources, but there is no magic with statistics. "No surprises" to me means a stable, consistent process robust to noise. The only way to assess robustness is to have the noise vary in your study. This also implies a time series. This is not the emphasis in experimentation where the time series is purposely compromised to accelerate understanding the model.
"The goal is to evaluate and remove insignificant components, then build an effective, predictive model within our design space."
Some word smithing...The goal is to build an effective (works), efficient (cost effective), useful (manageable), predictive (consistent & stable) model that is robust (to noise). Of course, you may want to consider the concept of continuous improvement? What happens as technology evolves? As new materials are developed or adapted? As measurement and measurement systems improve? As customer requirements change?
"it makes sense to me that each factor should have an optimum (A quadratic element) over a wide test range".
Why a quadratic? You only care about departures from linear when they are significant. It is much easier to manage a linear model. The objective isn't to get a model that exactly predicts. These models are often overly complex and only work over a narrow space.
"How do you know what interactions are important?"
I would start with the SME. What interactions make sense? What interactions are predicted? Why? (hypotheses). I would rank order the model effects up to 2nd order. As the 2nd order effects rise in the list, the need to increase the resolution rises. Classical orthogonal designs are quite useful in sequential work as the aliasing structure is known and it is not partial. While you may spend resources on more runs to start, it will be easier to de-alias in subsequent experiments. In any case, design multiple options for 9 factors (easily done in JMP). Evaluate what each design option will do in terms of what knowledge can be potentially gained (e.g., what effects will be separated, which will be confounded, which will not be in the study). Contrast these options with the resources required to complete. Predict ALL possible outcomes from each design. Predict what actions each possible outcome will result in. Select there design that you predict will be the best compromise between knowledge and resources. Run it. Be prepared to iterate (there iterations should be predicted).
"How do you know what interactions are being evaluated when using non-custom screening options?"
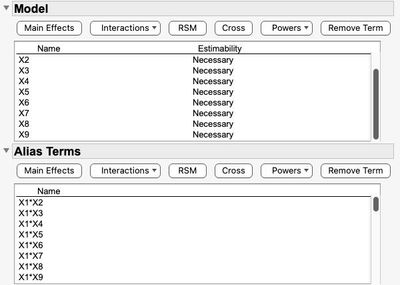
JMP will provide the aliasing structure for each proposed design.
I would agree, in general, the more "custom" your design, the more complicated the aliasing. This is the risk with partial aliasing. The reward is fewer runs in the current design. Is it fewer over the course of sequential experimentation? Who knows.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us