- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How to make a single variable non-linear design that has more than one condi...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to make a single variable non-linear design that has more than one condition
Hello - As with a lot of experimentalists, I've lost a lot of lab time over the last few months. Of course, DOE is a great way to make up that time if one wasn't planning of using it in the first place. We are working with models so standard DOE wont work. I tried doing the nonlinear design platform on JMP, but kept getting a single condition replicated 10 times. The model (y = f(x)) is y=q*K*x/(1+K*x), where q and K are parameters. Obviously a univariate linear model is nearly trivial to select conditions to test, but a univariate nonlinear model shouldn't be nearly as simple. Before Covid we were doing 15 or so conditions, 3 times each testing two dozen systems, taking a to two weeks per dataset to generate. I'd like to reduce the number of experiments, but I wouldn't want to reduce it too much without a statistical argument for doing so, as this research will be published.
How do I do this?
Thank you in advance.
P.S. Would prefer a non-scripting answer, but if there is no other answer, and learning how to script will take less time than doing this, I'm all ears.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
The 2 parameters define a function with a definite shape but infinite varieties. The parameter K appears in the numerator and the denominator. It defines the sharpness of the transition from the initial low value to the final high value of the function. So only two parameters are required. So only two levels of X are required to fit the model. (BTW, the linear model as you said requires p + 1 because of the intercept, another parameter.)
Here is a simple script for a simple demonstration of the function with different values for the parameters that you can use to see how the shape is defined.
Names Default to Here( 1 );
// initial model parameter values
q = 1.0;
K = 0.01;
// demonstration
New Window( "Langmuir Isothermal Adsorption",
Outline Box( "Graph",
gb = Graph Box(
X Name( "X" ),
X Scale( 0, 100 ),
Y Name( "Y" ),
Y Scale( 0, 1 ),
Y Function( (q*K*x) / (1+K*x), x )
)
),
Outline Box( "Model Parameters",
Line Up Box( N Col( 2 ),
Text Box( "q" ),
Slider Box( 0, 2, q,
gb << Reshow;
),
Text Box( "K" ),
Slider Box( 0.005, 0.05, K,
gb << Reshow;
)
)
)
);I was mistaken. The optimality criterion can be a useful aspect of design for the linear model. There is no choice for the non-linear model. It is D-optimal. This criterion minimizes the joint confidence region of the parameter estimates. That is to say, the design assures that your parameter estimates will have the smallest standard errors
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
I''d be happy to take a shot with some feedback, but realize you are asking about a specific situation and you really haven't provided us with enough information to fulfill your specific request.
1. Your quote "We are working with models so standard DOE won't work" does not make any sense to me. Analysis of most DOE's is typically done by entering a model into the fit model platform.
2. You have one variable that you want to test at multiple levels. How did you get to there being only one variable? Did you perform other iterations to filter down to this one variable? What about noise?
3. Testing at 15 levels (I'm not sure what exactly you mean by 15 conditions except you have only 1 variable) is basically trying to pick a winner. What we are typically trying to do is to be able to predict a response variable(s) by developing a mathematical model that is a simplification of what is probably a more complex response surface. Typically these model are developed with some hierarchy of model terms. First order linear effects, second order linear effects,...2nd order non-linear effects (quadratic), etc. Second order non-linear effects can be estimated with 3-levels, third order non-linear effects (cubic) can be estimated with 4-levels, etc. What order effect would you be trying to estimate with 15-levels? This would be virtually useless in the real world. If the 15 means something else, I still would question why 15?
4. It looks like have historically built in either replication or repeats of the "conditions". I can't tell which from your message? The reason for doing replication this is to either form a basis of random un-biased errors to test the significance of treatment effects or to assign the variation in to the noise changing between replicates (if you were doing blocks for example). Why are you doing replication? And why 3 replicates?
5. You mention 2 dozen "systems". What is a system? Why must you test over all of the systems?
6. The attached JMP data table has nothing in it but column labels.
7. A practical argument for reducing runs can be just as valuable as a statistical argument.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
Wow - I didn't expect much response. Thank you for taking the time to think through my question so much. Looking back, I definitely see some ambiguities and lack of info in my question. I'll try to respond to your points and make clarifications.
1. What I meant by this was that when I took my DOE class in grad school, it was entirely linear (ie. factorial) and quadratic (ie. Response Surface) designs. There wasn't at all a discussion of nonlinear modeling, so I assumed that, given that 1) I was using a nonlinear model and 2) it was a specific model conceived with a specific application in mind (adsorption from a fluid to a surface in this case) rather than a generic nonlinear model (whatever that would be as analogous to factorial designs), this would be nonstandard, even though the general idea of DOE would still apply. Maybe I have too narrow an understanding of DOE.
2. This is a very old model, dating back to the 1910's, describing adsorption of some species (atoms, molecules, etc) from a fluid to a surface. All that is included is the concentration of the adsorbing species. It is assumed that other parameters (pressure, temperature, acidity of the medium, etc) are constant. We are testing adsorption systems with this model at different temperatures. Presumably the parameters will be different at different temperatures.
3. You are correct. I should have used the correct terminology. Thank you for reminding me of that. We are currently testing 15 levels (3 replicates) of the single factor and fitting the model to it. To the second half of your question, this is where I am self-admittedly wholly ignorant. My understanding is that with a polynomial, the number of points needed to fit a line is equal to the order of the polynomial + 1. So linear (O=1) needs 2 points, quadratic needs 2,.... trigintic needs 31. But what about for any nonlinear? My first thought would be that we need the number of parameters+1. So in my specific example of whats called a "Langmuir Adsorption Isotherm," there are 2 parameters, so at least 3 levels would be needed. But that's entirely on intuition that didn't get past low 300 level math classes and a single graduate DOE class, so I'm happy to be corrected on that. The literature in this field, however, is replete with experiments that often use many, many, many levels, frequently more than we do, so using a 3 level (or even 2 level) DOE would need to have a statistical justification. And I don't have the statistics training to supply that well. If you have a reference or your own explanation, I would very much appreciated either or both.
4. So I may be misunderstanding your question, but we are doing what would probably go under split-plot (or strip plot, its hard to say because its very difficult to do either correctly in our setting, due to materials changing over time during prep, etc). But we aren't including batches in the model because it is a physical model that assumes we a hypothetical system with intrinsic constants rather than specific experimental plan that incorporates real world issues like batch to batch variation into a statistical framework. The reason for replicates is just to account for error. The experiments, given the setup, are prone to error because things like temperature are not as well controlled as the ideal case (even with expensive equipment, its very difficult), and so replicates are helping the error handling. Also, I personally haven't published papers, but some of the post-docs in my lab have stated that higher impact journals typically want replicates and 3 is a standard number. Maybe I misunderstood your question though.
5. As I explain to my mom, an english major, I "put metals on sand" :). Basically I'm adsorbing metal onto different materials to be used in catalysis. We have a set of 3 metals and 6 adsorbing materials. Each adsorbing material will interact with each metal differently, which in turn affects the catalytic "activity." In addition, each metal does different types of catalysis (though there is some overlap). Basically the metals do different sets of reactions, and then the adsorbing material, based on its interaction with the metal, will promote (or whatever the reverse of promote is) certain subsets of those reactions. Each metal-adsorbing material pair is what I'm calling a system. I've had the thought of making metal and adsorbing material each categorical variables, but then we enter the split/strip-plot world and I wouldn't even know where to begin in adding that to a model that is rationally derived from thermodynamic principles. To do that would add in dozens of material parameters and make the model functionally useless.
However, it would be interesting and very useful to take the parameters from the adsorption model for each system and then stick those into a statistical model where we can generally predict the parameters for the adsorption model by simply inputting into the final statistical model just the metals and adsorbing materials. But first we need the adsorption model parameters.
6. Ah. I took the nonlinear design example from the help file and just mimicked it. I don't know how to make it more useful than this discussion, because I think my issue is theoretical. Also, Mark Bailey correctly replicated the issue.
7. That makes sense. From what I have heard, however, a formal argument is better for publication.
Hopefully this answers your questions. Thank you again for your feedback.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
I hope that you have considered @statman's thought-provoking comments and questions already.
Can you be more specific about how you set up the nonlinear design? This method requires prior information, including the values of the model parameters that are likely. You provided the equation of your model. What did you use for parameter values? What did you use for the optimality criterion?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
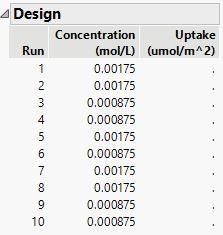
Here is an worked example. I use your model but I made up the rest.
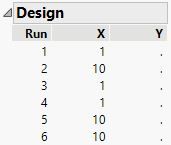
I want to observe and model Y over the range 1 to 10 of X. Here is my data table:
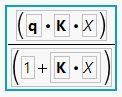
I have selected q = 10 and K = 2 for my prior parameter values to be used in your formula:
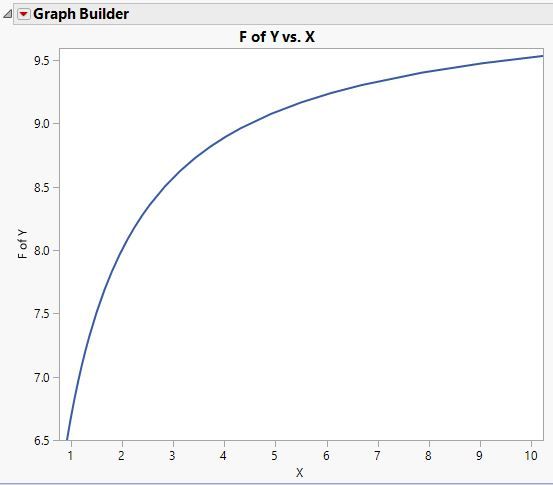
This set up leads to the following graph of the function, which is believed to be typical:
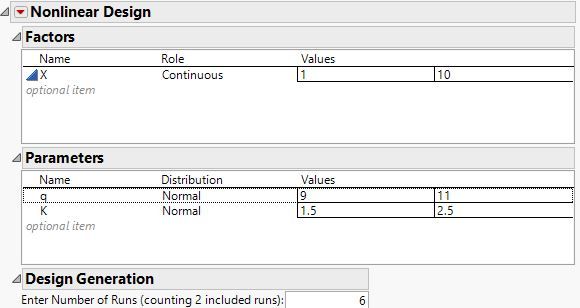
I initiate the design process and adjust range of likely priors:
Here is the optimal design for 6 runs:
As expected, the number of levels equals the number of parameters, 2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
Furthermore, using your data table verbatim and defaults in Nonlinear Design otherwise, I get this design, which contains more than one level:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
Mark - Thanks for taking the time to look into this.
Yes I redid my design and found what you said, it gives two levels.
To answer your questions, I set it up by inputting the factor, response, and model column, including an equation with parameters. I also coded the columns, as the example file for nonlinear designs did, and then I went through the menus to get the nonlinear design setup. I am now getting what you are getting, namely, 2 levels of the factor. I am not sure why it gave only 1 before. Sorry about that.
So you mentioned that there are two parameters, and therefore 2 levels. This makes sense in a linear model world, as I stated in my answer to @statman's feedback. But I could see an infinite number of models being generated from 2 levels for this specific model. In my mind, at the very least, there would need to be three levels to capture the sharpness of the point where the slope passes from >1 to <1. That point could be anywhere between (0,0) and (infinity, maxy), at least in my mind. I've looked into the theory of nonlinear, and it got into Fischer Information Matrices and I got very quickly in over my head. If my intuition is wrong about this, would you be able to explain why?
Also, to answer an earlier question you had,
1. My initial parameter values are around q=1 and K = 0.01 (that's very rough but the scale should be correct, depending on the units you use).
2. I wouldn't know where to begin with optimality criterion. I played around with the two option submenus that had to do with monte carlo sphere's, but that is something I know exactly zero about, and the JMP documentation assumed some knowledge that I didn't have. If you have an explanation and/or references, I'd love to hear it. If you're referring to D/I/etc-optimality, I don't remember seeing a submenu for that and even if I did, I wouldn't know how to apply it. My one DOE class was didn't got terribly far into theory. How would one apply it here?
Thank you for your comments and help. Its all very appreciated.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
The 2 parameters define a function with a definite shape but infinite varieties. The parameter K appears in the numerator and the denominator. It defines the sharpness of the transition from the initial low value to the final high value of the function. So only two parameters are required. So only two levels of X are required to fit the model. (BTW, the linear model as you said requires p + 1 because of the intercept, another parameter.)
Here is a simple script for a simple demonstration of the function with different values for the parameters that you can use to see how the shape is defined.
Names Default to Here( 1 );
// initial model parameter values
q = 1.0;
K = 0.01;
// demonstration
New Window( "Langmuir Isothermal Adsorption",
Outline Box( "Graph",
gb = Graph Box(
X Name( "X" ),
X Scale( 0, 100 ),
Y Name( "Y" ),
Y Scale( 0, 1 ),
Y Function( (q*K*x) / (1+K*x), x )
)
),
Outline Box( "Model Parameters",
Line Up Box( N Col( 2 ),
Text Box( "q" ),
Slider Box( 0, 2, q,
gb << Reshow;
),
Text Box( "K" ),
Slider Box( 0.005, 0.05, K,
gb << Reshow;
)
)
)
);I was mistaken. The optimality criterion can be a useful aspect of design for the linear model. There is no choice for the non-linear model. It is D-optimal. This criterion minimizes the joint confidence region of the parameter estimates. That is to say, the design assures that your parameter estimates will have the smallest standard errors
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to make a single variable non-linear design that has more than one condition
Hey Mark - Thanks for working with me on this. So that makes sense. I did actually think about the p+1 being because of the intercept after I replied a few days ago. Thanks for pointing that out. Ok, this all is making more sense now. I will take this back to my coworkers and we will come up with a plan. Thank y'all so much for your help.
Edward
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us