- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to get 95/99 Tolerance Interval for Non-normal Distribution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to get 95/99 Tolerance Interval for Non-normal Distribution?
Hi,
I have the current data set and it passes the goodness of fit for SHASH and Weibull distribution. I am looking to calculate the 95/99 Tolerance interval for this data set. I have similar data set for other attributes which may pass other non-normal distributions. Is there a easy way to calculate these non-normal tolerance intervals in JMP.
Thanks,
ABD
| 52.5 |
| 54.7 |
| 57.5 |
| 52.5 |
| 65.3 |
| 64.1 |
| 67.2 |
| 75.0 |
| 67.5 |
| 60.0 |
| 65.6 |
| 69.1 |
| 63.1 |
| 62.2 |
| 64.1 |
| 66.3 |
| 66.3 |
| 66.3 |
| 67.5 |
| 62.5 |
| 59.4 |
| 64.7 |
| 63.4 |
| 66.3 |
| 70.9 |
| 66.9 |
| 66.3 |
| 64.4 |
| 63.4 |
| 62.8 |
- Tags:
- windows
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
Tolerance interval is not a straight forward subject. The answers for Normal might be easy to find, but not for others. My answer may not be easy.
To my knowledge, the most comprehensive book that includes this subject is "Statistical Intervals" 2nd. ed. by Meeker, Hahn, and Escobar.
When we talk about this subject, things need to be clear:
- Meaning of the two percentage numbers. I am not sure what does the convention of 95/99 mean. But one number should mean the proportion of the population that the interval should enclose, and the other number means confidence level. Following assumes 95 means the confidence level, 99 means the other.
- One-sided bounds or two-sided intervals. The answers to and the reasoning behind the different types are quite different. One thing worth pointing out is that two-sided intervals are not uniquely defined, though there are conventions. They are only uniquely defined if the two tail proportions are defined. And equal proportion might be a convention, but that could be wrong in practice if the risk of being wrong costs differently in two tails.
- If the concern is about a one-sided bound, the lower tolerance bound to enclose at least 99% of a population with 95% confidence level, is the same as the lower 95% confidence bound of the (1-99%)=1% quantile estimate.See section 2.4 of the book. The upper tolerance bound is similarly defined.
- If the concern is about a two-sided interval with equal tail probabilities, an approximation to the lower and upper bounds includes lower 97.5% confidence bound of 0.5% quantile estimate and upper 97.5% confidence bound of 99.5% quantile estimate. See section 12.7 of the book.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
Thanks for your reply. My query was to find tolerance interval for 99% population with 95% confidence for non normal data sets. For the data set above I am looking for a two sided interval
Another statistical platform (for which I only have a demo version) is able to give this solution quite easily. But , say I want to get the same result in JMP, I was wondering how to do that. I have tried transforming the data to Weibull distribution (for above data set), but back calculating limits in original data format is becoming challenging. I have a large number of attributes and different non-normal distributions pass for the goodness of fit for different attributes. Thus, I am looking for steps which can help me calculating these non-normal tolerance intervals in JMP.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
Here are the options that I see.
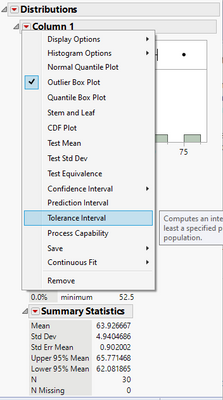
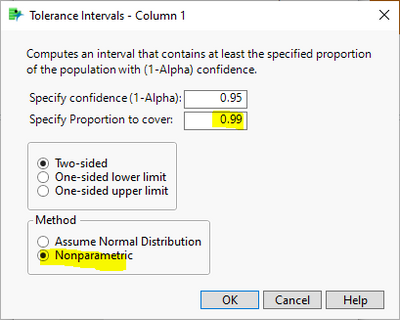
First, the Distribution platform. Choose "Tolerance Interval" item, then choose "Nonparametric" method. See next two screenshots.
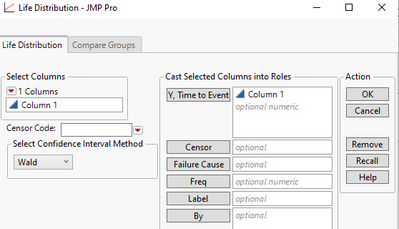
Second, the Life Distribution platform. This platform was not designed to answer tolerance interval questions specifically. But I have explain how it can be repurposed via confidence intervals.
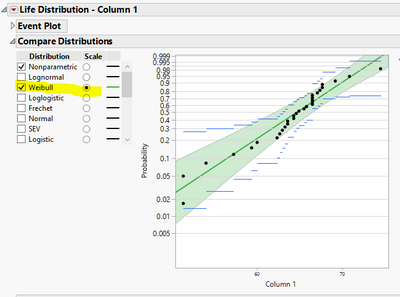
1.First launch the platform, the item is under Analyze > Reliability and Survival > Life Distribution. Configure dialog, and your data column goes into Y.
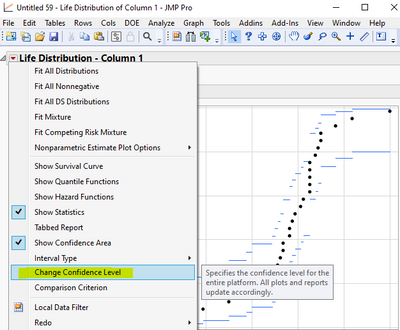
2. Change Confidence Level to 0.975. (Ignore the title shows 98% due to rounding in display, which is a bug I just noticed now. Ignore if column title organization may look different in your version, there is a change in the layout in JMP17.)
3. If Weibull is desired, first fit Weibull, and seems that your data fits the distribution well.
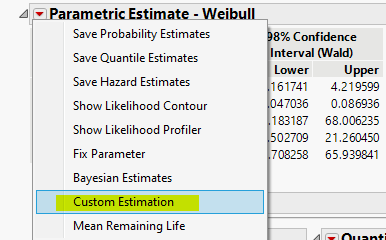
4. Choose "Custom Estimation" from the distribution result's menu.
5. Choose "Lower" in the following menu.
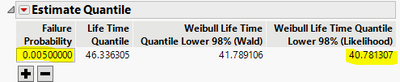
6. Enter 0.005 in the Probability. Record the lower bound.
7. Now change to "Upper"
8. Enter 0.995 in the Probability. Record the upper bound. You may want to consider using Likelihood type bound for your sample size.
The two bounds are the ones that I explained in item 4 of my previous response.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
Just to re-visit this topic. My understanding is that there can be several approaches in estimating tolerance intervals for non-normal distributions. Could the following be one appropriate approach?:
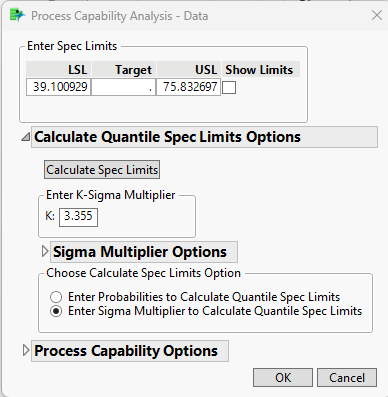
1. Get k-factor used to estimate the Normal DSN tolerance intervals. In this case it would be k=3.3546 for N=30, 2-sided, C=0.95, p = 0.99;
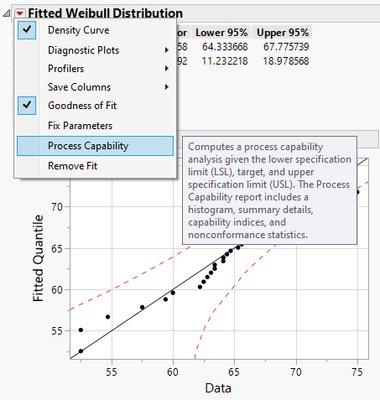
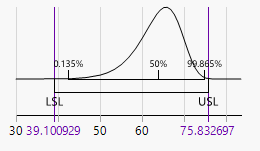
2. Use this k-factor to get equivalent probabilities in the fitted non-normal distribution by translating the K-sigma normal probabilities into the respective quantiles. JMP has this capability in Process Capability > Calculate Quantile Spec Limits Options > Enter K-Sigma Multiplier in Analyze > Distribution. Below is shown for the Weibull DSN as an example. It calculates corresponding quantile spec limits (39.100929 and 75.832697). My question is can these calculated spec limits be interpreted as viable tolerance intervals?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
I am not specialized in SPC. I cannot answer your question without further research. Maybe the experts in the community can help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
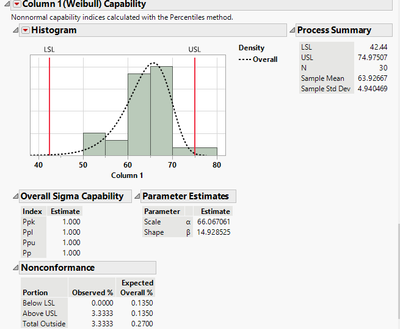
Hi @ashwint27 : I would not do it that way. You can see why by putting in 3 as your K-Sigma multiplier. If you do that you'll get the results below. As you can see, K=3 corresponds to your garden-variety "+/- 3Sigma" as the Expected Overall % Total Outside is 0.27% (recall, "mean +/- 3Sigma" covers 99.73% of the population in the normal case) . If this method is correct, the Expected Overall Total Outside would be larger than 0.0027% to account for the fact that you are estimating the mean and Sigma. So, the interval as you've calculated here is not taking the variability in the estimates into account; i.e., mean +/- 3Sigma covers 99.73% of the population (assuming normality) if the population mean and Sigma are known...and they never are. That's what separates tolerance intervals from the garden-variety (and ubiquitous/misleading/misused/abused) "+/-3Sigma".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
This is how I do it.
Step 1: Fit the distribution to the data. For example, with a Weibull distribution you will get parameters alpha and beta.
Step 2: Lets say I want a two-sided 99% tolerance. For each side of the distribution I want 0.5% outside.
Step 3: I use the JSL script editor as a calculator:
lower = Weibull Quantile( 0.995, beta, alpha);
upper = Weibull Quantile( 0.005, beta, alpha);
show(lower,upper)- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to get 95/99 Tolerance Interval for Non-normal Distribution?
Hi @David_Burnham : A good estimate if your sample size is large enough, but like @ashwint27 proposed method above, this method suffers from using estimates in place of population parameters. Directly related to that, where does the 95% confidence come in?
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us