- JMP will suspend normal business operations for our Winter Holiday beginning on Wednesday, Dec. 24, 2025, at 5:00 p.m. ET (2:00 p.m. ET for JMP Accounts Receivable).
Regular business hours will resume at 9:00 a.m. EST on Friday, Jan. 2, 2026. - We’re retiring the File Exchange at the end of this year. The JMP Marketplace is now your destination for add-ins and extensions.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to estimate standard deviation for large population from small samples size
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to estimate standard deviation for large population from small samples size
Hi
If I have the distribution of data from small sample size (e.g. N=250, 1000), and would like to estimate the distribution (e.g. sigma) of data on large population (e.g. N=1 million)? What is the confidence level / error on the prediction ?
(Assume the distribution is Normal distribution or same shape for small/large population)
Thanks!
Kelvin
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to estimate standard deviation for large population from small samples size
Hi Kelvin,
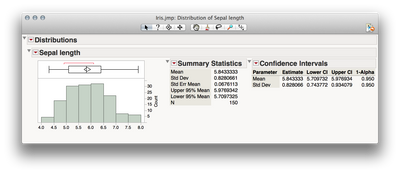
To obtain confidence intervals for the standard deviation in JMP you can use the distribution platform. Here are steps to obtain those confidence limits:
From an open table:
1. Analyze > Distribution
2. Cast your variable of interest to the Y role and click OK
3. From the Red Triangle next to your variable name, select Confidence Interval
4. Select your desired level of confidence
The resulting table will display the confidence limits for both the mean and the standard deviation (as shown in the screenshot below). With sample sizes you described your intervals will probably be quite narrow. The size of the population from which the sample was drawn is irrelevant in this approach, and unless the sample size is some sizable proportion of the population size (e.g. 0.50 of the population) there are no "corrections" to this confidence interval necessary.
I hope this helps!
Julian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to estimate standard deviation for large population from small samples size
Hi Kelvin,
To obtain confidence intervals for the standard deviation in JMP you can use the distribution platform. Here are steps to obtain those confidence limits:
From an open table:
1. Analyze > Distribution
2. Cast your variable of interest to the Y role and click OK
3. From the Red Triangle next to your variable name, select Confidence Interval
4. Select your desired level of confidence
The resulting table will display the confidence limits for both the mean and the standard deviation (as shown in the screenshot below). With sample sizes you described your intervals will probably be quite narrow. The size of the population from which the sample was drawn is irrelevant in this approach, and unless the sample size is some sizable proportion of the population size (e.g. 0.50 of the population) there are no "corrections" to this confidence interval necessary.
I hope this helps!
Julian
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us