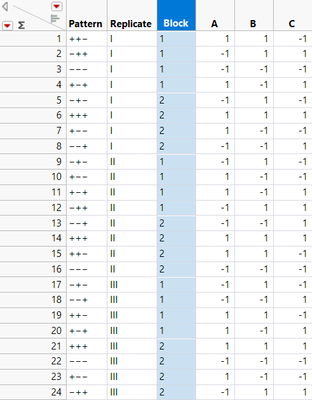
in DOE it is possible to construct a design which has multiple replicates and each replicate confounded a different effect，by this way you can evaluate the effect confounded by the replicates not confounded with this effect. but i dont known how to construct such design and how to analysis it by jmp.
a design like this：
Accepted Solutions
Hi @ZHANDOUJI,
It's hard to tell how to reproduce the design without showing the resulting datatable.
However, based on the informations provided, it seems that the 24-runs design for 3 factors seems to be composed of three classical 8-runs factorial designs with different generating rules (because of the differences in confounding patterns) and 2 blocks for each.
Here is how to create the first 8-runs design :
- Use the platform Screening Designs, specify three continuous factors A, B and C, and use the option "Choose from a list of fractional factorial designs" to choose the 8-runs factorial design with 2 blocks (4 runs per block) :
Then, in the Generating rules, make sure that Block is confounded with A, B and C (all cases are checked) :
You can verify that the interaction A*B*C is confounded with the block by clicking in the red triangle of the "Aliasing of Effects" panel and showing the aliasing pattern up to the third order :
You can then click on "Make Table" to generate the first part of the 3-parts design.
- For the second 8-runs design part, the process is the same, but the Generating rules are different to enable the confounding between the Block and the A*B interaction :
- For the third part, same process, but again you'll have to change the generating rules and check cases B and C only so that the block effect can be confounded with interaction B*C.
At the end, concatenate all designs into one table, and add a column indicating the replicate number (I, II and III for the three design parts) :
To build the model with the same degree of freedoms as you have shown in your capture, you have to add all main effects, 2-factors interactions and the 3-factors interaction, the Replicate effect, and the Block effect nested in the replicate effect :
When using this model on a response (I used a random normal formula just for illustration), you can see in "Effect Tests" and "Analysis of Variance" panels that you have the same degrees of freedom to estimate the terms needed as in your capture :
I attach the final datatable with the three design parts concatenated with a script to launch the specific model with adequate terms.
Hope this answer will help you,
Hi @ZHANDOUJI,
It's hard to tell how to reproduce the design without showing the resulting datatable.
However, based on the informations provided, it seems that the 24-runs design for 3 factors seems to be composed of three classical 8-runs factorial designs with different generating rules (because of the differences in confounding patterns) and 2 blocks for each.
Here is how to create the first 8-runs design :
- Use the platform Screening Designs, specify three continuous factors A, B and C, and use the option "Choose from a list of fractional factorial designs" to choose the 8-runs factorial design with 2 blocks (4 runs per block) :
Then, in the Generating rules, make sure that Block is confounded with A, B and C (all cases are checked) :
You can verify that the interaction A*B*C is confounded with the block by clicking in the red triangle of the "Aliasing of Effects" panel and showing the aliasing pattern up to the third order :
You can then click on "Make Table" to generate the first part of the 3-parts design.
- For the second 8-runs design part, the process is the same, but the Generating rules are different to enable the confounding between the Block and the A*B interaction :
- For the third part, same process, but again you'll have to change the generating rules and check cases B and C only so that the block effect can be confounded with interaction B*C.
At the end, concatenate all designs into one table, and add a column indicating the replicate number (I, II and III for the three design parts) :
To build the model with the same degree of freedoms as you have shown in your capture, you have to add all main effects, 2-factors interactions and the 3-factors interaction, the Replicate effect, and the Block effect nested in the replicate effect :
When using this model on a response (I used a random normal formula just for illustration), you can see in "Effect Tests" and "Analysis of Variance" panels that you have the same degrees of freedom to estimate the terms needed as in your capture :
I attach the final datatable with the three design parts concatenated with a script to launch the specific model with adequate terms.
Hope this answer will help you,