- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- Re: How to check the aliasing term in DOE custom design
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to check the aliasing term in DOE custom design
Hi Anyone,
How do we check what is the confounding factors during our initial custom design setup?
Rgrds
Irfan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
Custom design will seldom give you a design with perfect aliasing. So the report will use correlations to show you the degree of aliasing that is present.
When creating the design, notice just below the model window is the "Alias Terms" part of the report. Open that up and put in the terms for which you wish to check for aliasing. For example, if the model has only main effects and you wish to see if they are aliased with two-factor interactions, then put the two-factor interactions in the Alias Terms window.
Now, when you generate the design, under Design Evaluation, you will see the Alias Matrix as an option. Opening that up will show you the correlations between your model terms and the alias terms specified earlier. A value of 1 would show complete aliasing. Any non-zero term shows "partial" aliasing. Graphically, you can see this on the color map on correlations report.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
Thanks Dan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
Hi Anyone,
Able to explain to me what does the 'Temperature is biased by 0.333 times the true value of the grind*time? Does it mean that the parameter estimates for temperature is 1/3 value of the grind*time estimates?
Rgrds
Irfan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
Irfan,
This links walks through an example of the effects of confounding (also called aliasing or partial aliasing)
https://en.wikipedia.org/wiki/Fractional_factorial_design
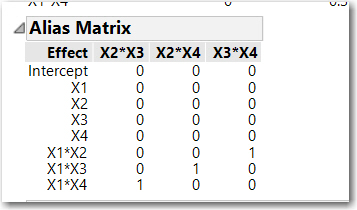
For another example, I have attached 4-factor fractional factorial. The screenshot below displays the alias matrix. The response Y was created from the formula
20 + 1*:X1 + 2*:X2 + 3*:X3 + 4*:X4 + 0.5*:X12 + 1*:X34 + 5*:X13 -5*:X24 +5*:X14 +10*:X23 + 1*Random Normal()Since X12 (simpler notation) is confounded with X34, and only X12 is in the model, it's coefficient should be approx. 1.5. And since X13 and X24 are correlated the coefficient of X13 will be approx. 0, and the coefficient of X14 will be approx. 15. This is why checking the evaluating the design which includes checking the alias structure is an important step in designing an experiment. If there is an expected important interaction, the design should be chosen so it has no confounding with other 2 factor interactions, or small partial interactions with multiple effects.
Georgia
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
The correlation of 0.333 means that the estimated effect of Temperature is increased by the effect of the gind*time-interaction multiplied by 1/3. So basically you are estimating in the analysis
[Temperature] = Temperature + 1/3*Grind*Time
Thus if there is a strong interaction effect it will inflate your main effect estimator.
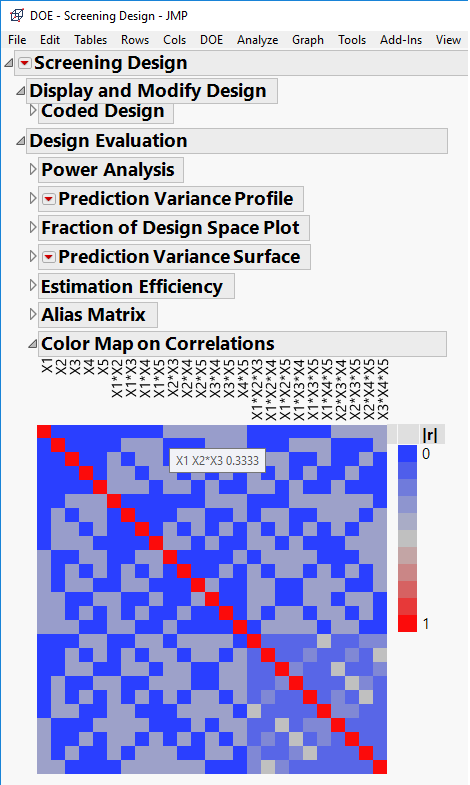
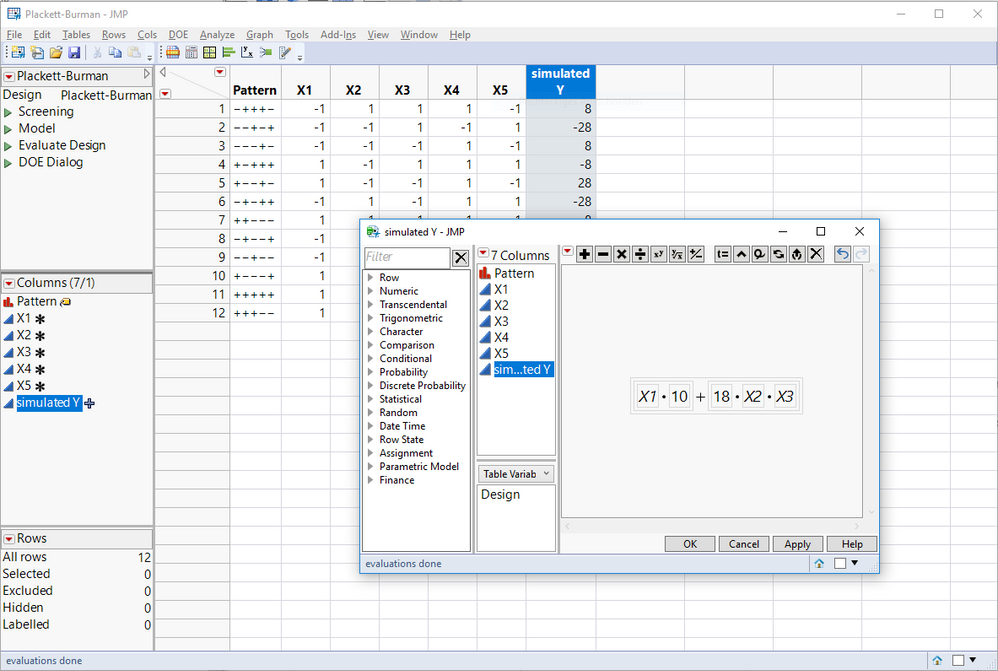
You can see that by simulating some simple data. For demonstration purposes I will use a Plackett-Burrman screening design with the following correlation structure:
As you can see the main effect X1 has a correlation of 0.333 with the X2*X3-interaction. I generated the design and added some simulated data:
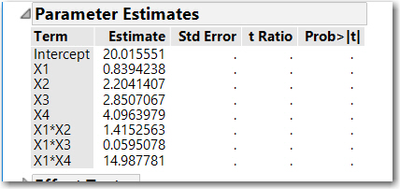
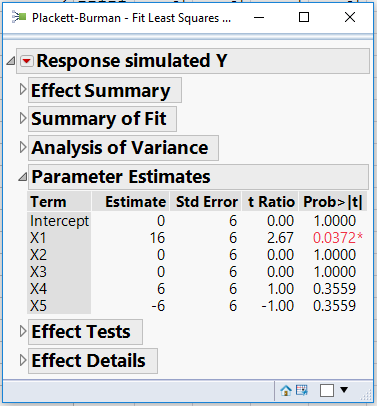
As you can see, the true effect of X1 = 10, the true effect of the interaction X2*X3 = 18. If we now fit a main effects model you get the following results:
The estimated effect of X1 = 16, which is the true effect of X1 - which is 10 - and it is biased by 1/3*18 (the effect of X2*X3).
Hope this helps.
Sebastian
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
Hi Sebastian,
Does it mean that if I have a correlation of -1 for X2*X3 with X1 then it might cancel out the estimated effect of X1?
Rgrds
Irfan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to check the aliasing term in DOE custom design
You are correct. This might as well happen if you find a correlation of 1 and a negative effect of X2*X3 and a positive effect of X1.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us