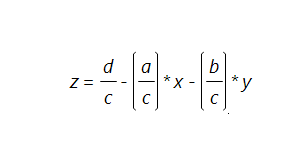- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Discussions
Solve problems, and share tips and tricks with other JMP users.- JMP User Community
- :
- Discussions
- :
- How to best fit data to a plane or line
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
How to best fit data to a plane or line
Hello
I was wondering if there is a way in JMP that I could use to take raw data of multiple measurement points (each with an X, Y, Z component) and best fit this data to form a best fit plane. Basically my intent is to take raw metrology data off of OMMs/CMMs and fit them myself without the use of CMM/OMMs measurement software.
Thanks for your help!
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to best fit data to a plane or line
I used ax + by + cz = d as a starting point to generate some slightly random data like this:
dt = New Table( "Untitled",
Add Rows( 20 ),
New Table Variable( "a", 5 ),
New Table Variable( "b", 7 ),
New Table Variable( "c", 11 ),
New Table Variable( "d", 13 ),
New Column( "x", Formula( Random Uniform() * 10 ) ),
New Column( "y", Formula( Random Uniform() * 10 ) ),
New Column( "z", Formula( Random Normal() / 2 + (:d - (:a * :x + :b * :y)) / :c ) )
);
which makes Z a function of X and Y, approximately on the plane defined by A, B, C, D.
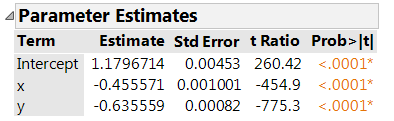
Next, use Analyze->Fit Model and put in Z as the Y (response) and ADD X and Y to the model effects. Click Run. The parameter Estimates are what I think you are looking for. I get this, for my random numbers:
to convert these back to the A=5, B=7, C=11, D=13 form, rearrange the formula as
and see d/c is 13/11 is 1.1818 (close to 1.179) a/c is 5/11 is .4545 (close to .4555) and b/c is 7/11 is .6363 (close to .6355). Watch the signs. You can see the surface in the Fit Least Squares window; red triangle menu->Factor Profiling->Surface Profiler. Under Appearance turn on the Actual points.
In the platform you can rotate the surface to clearly see the points above and below the plane. Try clicking the points to select them. This picture doesn't do it justice...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to best fit data to a plane or line
I used ax + by + cz = d as a starting point to generate some slightly random data like this:
dt = New Table( "Untitled",
Add Rows( 20 ),
New Table Variable( "a", 5 ),
New Table Variable( "b", 7 ),
New Table Variable( "c", 11 ),
New Table Variable( "d", 13 ),
New Column( "x", Formula( Random Uniform() * 10 ) ),
New Column( "y", Formula( Random Uniform() * 10 ) ),
New Column( "z", Formula( Random Normal() / 2 + (:d - (:a * :x + :b * :y)) / :c ) )
);
which makes Z a function of X and Y, approximately on the plane defined by A, B, C, D.
Next, use Analyze->Fit Model and put in Z as the Y (response) and ADD X and Y to the model effects. Click Run. The parameter Estimates are what I think you are looking for. I get this, for my random numbers:
to convert these back to the A=5, B=7, C=11, D=13 form, rearrange the formula as
and see d/c is 13/11 is 1.1818 (close to 1.179) a/c is 5/11 is .4545 (close to .4555) and b/c is 7/11 is .6363 (close to .6355). Watch the signs. You can see the surface in the Fit Least Squares window; red triangle menu->Factor Profiling->Surface Profiler. Under Appearance turn on the Actual points.
In the platform you can rotate the surface to clearly see the points above and below the plane. Try clicking the points to select them. This picture doesn't do it justice...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to best fit data to a plane or line
Thanks for the response. I used the fit model platform as instructed and it worked perfectly.
Do you have any ideas on how to un-fit the data? Basically if I have X, Y and the equation for Z is there a way to determine what the original Z was?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to best fit data to a plane or line
red triangle->SaveColumns->PredictionFormula will add a formula column to the table which shows the predicted value for an (X,Y). It will generally not be exactly the same as any of your original data points. Perhaps what you want to see is the differences between the original and predicted column...saveColumns->Residuals.
It sounds like you might want something else though. Can you explain what you are trying to do? A graph perhaps, similar to the surface plot? Or some sort of query system to retrieve the data?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Get Direct Link
- Report Inappropriate Content
Re: How to best fit data to a plane or line
I think the answer also depends on exactly what is meant by ‘best fit’. When there is no natural distinction between predictor and response variables, or when all variables are measured with error you should consider principal components analysis. This is in contrast to the usual regression assumption that predictor variables (taken as X and Y above) are measured exactly, and only the response variable (taken as Z above) has an error component.
Recommended Articles
- © 2026 JMP Statistical Discovery LLC. All Rights Reserved.
- Terms of Use
- Privacy Statement
- Contact Us